| Imaginez
une surface où les deux faces n'en font qu'une... vous
arrivez de l'autre côté sans jamais changer de
face.
C'est le ruban de Möbius.
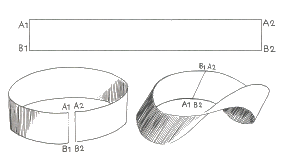
Prenez une longue bande de papier mince et reliez les extrémités
après avoir fait un demi-tour avec l'une des extrémités
comme indiqué ci-contre.
Vous avez un ruban de Möbius, du nom d'August
Möbius qui en publia une construction en 1865.
"Sa forme symbolise l'équilibre entre nos moi intérieur
et extérieur".
|
|
Suivez la
mouche... le ruban n'a qu'un seul bord.
CLIQUER
Si d'un point
quelconque on trace une ligne dans une direction ne coupant pas le
bord on se retrouve à mi-chemin au point de départ mais
de l'autre côté du papier. Continuons, après
un autre tour alors on se retrouve au point de départ et du
même côté.
Suivez la
mouche... le ruban n'a qu'une seule face.
CLIQUER
Comme il n'a qu'une face, un tapis roulant qui aurait subi
un demi-tour, comme celui breveté par la société
Goodrich Tyre Company, s'usera régulièrement des deux
côtés.
Plusieurs
marques d'imprimante
matricielle utilisaient des cassettes avec un ruban de Möbius.
Le ruban était donc encré des 'deux' côtés.
Le pli du ruban était commandé par une languette de
plastique située juste avant sa sortie.
Certaines personnes assez ingénieuses réencraient donc
ce ruban jusqu'à une dizaine de fois, avec une encre de qualité,
de bons gants et surtout une bonne dose de savoir faire !
Beaucoup d'usagers ignoraient évidemment que leur cassette
contenait un ruban de Möbius.
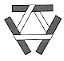
On
peut tendre une bande cylindrique entre deux rouleaux.
Pour le ruban de Möbius il en faut trois. |
 |
Maintenant si l'on découpe
ce ruban le long de sa ligne médiane, on n'obtient pas deux morceaux
mais un seul formant quatre demi-tours comme si les extrémités
de la bande avaient subi deux tours complets avant d'être assemblées.
Les bords forment maintenant deux courbes distinctes, reliées
l'une à l'autre, mais chacune sans aucun nœud.
Suivez la
mouche... il n'y a qu'un seul ruban.
CLIQUER
Et maintenant coupez la bande de Möbius au tiers de sa largeur
et observez...
| Le
vase de Klein est une surface fermée à une seule
face; elle n'admet ni intérieur, ni extérieur
et n'est pas orientable. De façon très imagée,
on obtient cette surface en allongeant le col d'une bouteille
et en le raccordant par l'intérieur avec le fond après
lui avoir fait traverser la bouteille. (Dictionnaire des
mathématiques de A.Bouvier.M.Georges et F.Le Lionnais.)
|
|