Le casse-tête

Bernard Monteil fabrique pour le plaisir de magnifiques solides.
Ces belles réalisations sont intrigantes :
chaque pièce est encastrée dans une autre.
Et les différentes parties sont bien entendu réalisées dans une seule et même pièce de bois.

En voici trois beaux exemples avec des dodécaèdres ou des cubes encastrés.


En voici trois beaux exemples avec des dodécaèdres ou des cubes encastrés.

      

Intéressons-nous aux cubes et smplifions la construction en ne gardant qu' un seul petit cube tout juste inscrit dans une sphère ou simplement dans un grand cube.
Le petit cube sera simple et n'aura pas de pointes. Le grand cube sera découpé le plus simplement possible.

Intéressons-nous aux cubes et smplifions la construction en ne gardant qu' un seul petit cube tout juste inscrit dans une sphère ou simplement dans un grand cube.
Le petit cube sera simple et n'aura pas de pointes. Le grand cube sera découpé le plus simplement possible.

QUESTION

Comment procéder mathématiquement pour construire un cube de 4 cm d'arête, inscrit dans un cube de 6 cm d'arête ?
Même question avec un grand cube de 50 mm d'arête et un petit cube de 24 mm d'arête.



SOLUTION

Il suffit de découper sur chaque face du grand cube un cylindre.
Ce cylindre aura bien entendu une profondeur (dite hauteur du cylindre) et un diamètre particuliers.

A l'adresse suivante on trouve une vidéo en anglais mais totalment compréhensible ne observant :
https://www.youtube.com/watch?v=TfV_APBk16Q

Bien placé le petit cube peut tout juste être extrait du grand.
Dès qu'on le tourne un peu à l'oblique, il sera bloqué dans le grand cube.

MAGIQUE ce petit cube encastré obtenu en découpant des disques ;).

Ces photos du travail de Bernard Monteil explicitent le découpage :

                  




Mathématiquement, voici comment déterminer très simplement les mesures

La base des cylindres est un disque. Les disques de chaque face sont deux à deux orthogonaux (perpendiculaires).
Et deux à deux, ils se coupent en un segment de droite qui deviendra le côté d'un carré.
Enfin ce segment sera l'arête du petit cube inscrit que nous allons obtenir.
Cette arête devra mesurer 4 cm.

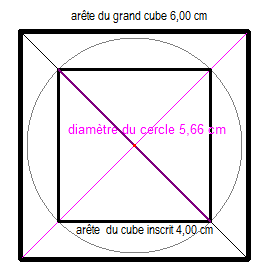
Le diamètre du cercle à découper est l'hypoténuse d'un triangle rectangle isocèle de côté 4cm.
En utilisant le théorème de Pythagore, il est facile de voir que la mesure de ce diamètre est égale à 4 cm soit environ 5,66 cm.
Chaque disque à découper sera centré au point d'intersection des diagonales des faces du grand cube.
Dans ce cas, il faut bien dire que le grand cube ne sera pas très épais... puisque seulement de 3,3 mm

L'épaisseur ou hauteur du cylindre correspondra exactement à l'écart entre le petit cube et le grand, c'est-à-dire à l'espace entre les deux carrés.
Pour cela, il faut imaginer les deux plans perpendiculaires de deux faces.

Dans cet exemple ce sera exactement( 6 - 4) / 2 = 1 cm.

Le cylindre a à découper sur chaque face dans cet exemple sera de 1 cm d'épaisseur et de diamètre environ 5,66 cm soit exactement 4 cm.

Il y a comme on le voit sur l'exemple précédent des limites entre les dimensions des deux cubes.
Si a est la mesure de l'arête du grand cube et b celle du petit cube.

Il faut que b < a, (soit environ 1,414*b < a) sinon la construction n'est pas possible puisque le diamètre du cylindre à découper serait plus grand que l'arête du grand cube.

Autre exemple correspondant à celui des photos de B. Monteil : 50 mm et 24 mm
Le disque à découper est de diamètre 24 (environ 34mm) et il est d'épaisseur (50 - 24) /2 = 13 mm.


ANIMATIONS

ATTENTION chacune de ses deux animations utilise beaucoup de mémoire de calcul.

Elles tournent de façon beaucoup plus fluide si on "manœuvre" les solides en utilisant les flèches du clavier.
Cliquer d'abord dans le cadre de l'animation puis "manœuvrer".
Passer la souris sur les consignes pour les explications.



Cette première animation, essaie de montrer comment l'intersection de disques délimite un cube à l'intérieur du grand.

CLIQUER

Cette deuxième animation essaie de montrer en transparence les cylindres découpés.
Cliquer Glisser l'objet pour trouver un point de vue explicite...

CLIQUER