Problème

Ce petit problème m'a été envoyé par un visiteur.
Malheureusement son courrier a été effacé lors d'une malencontreuse manœuvre et je n'ai donc pas pu répondre.

Aussi ai-je transformé ce courrier en petite énigme pour me faire pardonner.
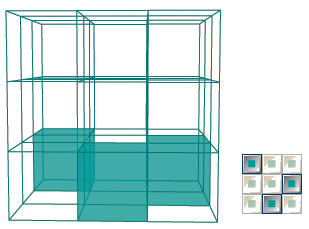
Nous avons un grand cube composé de 27 petits cubes transparents.
On dispose de cubes verts devant remplacer certains cubes transparents.
Il faut remplacer le plus petit nombre possible de cubes transparents par des verts afin que le grand apparaisse complètement vert
lorsqu'on le regarde frontalement (perpendiculairement) sur chacune des six faces.
Les vues de face, de côté et de dessus doivent paraître vertes.

Combien allons-nous prendre de cubes verts ?

ATTENTION, l'animation suivante donne le cube en perspective et selon l'angle de vision, l'opacitépeut disparaître logiquement.
A chacun de bien orienter son cube pour obtenir chaque vue de face, de profil et de dessus.
Les carrés sur le côté correspondent à chaque étage du grand cube dans une certaine position.

Généraliser le problème à un grand cube de n³ petits cubes.

Un clic colorie un petit cube en vert. Un autre clic supprime la couleur.

CLIQUER

SOLUTION Le nombre minimum de petits cubes à colorier en vert est 9. Voici une disposition possible de ces cubes sur les trois niveaux. Pierre Jullien propose très astucieusement de raisonner en utilisant un algorithme de carré latin. Par exemple pour un cube de 27 : 0 1 2 1 2 0 2 0 1 Ceci signifie que sur le niveau 0 en bas, on place des cubes verts aux places indiquées par le n° 0 ; pour le niveau 1 du milieu, on place les cubes verts aux places indiquées par le n° 1 ; pour le niveau 2 en haut, on place les cubes verts aux places indiquées par le n° 2. La solution proposée ci-contre correspond au carré latin indiqué ci-dessus. Pour un cube de n3 petits cubes, il suffit de colorier en vert n² petits cubes. On utilise le même algorithme, par exemple : 0 1 2 3 1 2 3 0 2 3 0 1 3 0 1 2 Cf la solution généralisée de Diophante ICI.

Voici de face une représentation du cube précédent colorié seulement niveau par niveau.

La base horizontale du cube seule :	L'étage n°1 seul :
L'étage n°2 du haut seul :

---