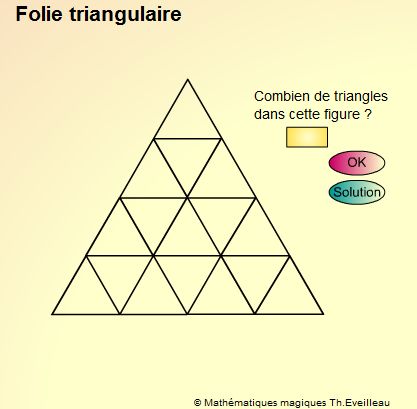CLIQUER

 

 

 

 

SOLUTION


Il y a 1 triangle dans le cas 1,
il y en a 5 dans le cas 2, et
13 dans le cas 3,
puis 27...

De façon générale pour un triangle de côté n, nous trouvons,

- si n est pair : n(n+2)(2n+1)/8

- si n est impair : [n(n+2)(2n+1) -1]/8

Ce résultat peut se démontrer par récurrence sur n.

En effet si n est pair, on passe d'une figure de côté n à la suivante en ajoutant
[1 + 2 +... + (n+1)] triangles (autant que de points de la figure numéro n) et
[n + (n-2) +... 2 + 0 ]=(n/2)(n/2 +1) triangles dont l'un des sommets est sur le grand côté horizontal.

Et si n est impair, on passe d'une figure de côté n à la suivante en ajoutant
[1 + 2 +... + (n+1)] triangles (autant que de points de la figure numéro n) et
[n + (n-2) +... 3+ 1]=[(n+1)/2]² triangles dont l'un des sommets est sur le grand côté horizontal.