Problème
Lors
d'une soirée, les invités ont tous serré la main
de trois autres invités, excepté l'un d'entre eux qui
n'a donné qu'une seule poignées de mains.
Il s'agit avec ces seules informations de répondre aux questions
suivantes :
1° Quel est le plus petit nombre d'invités,
possible de cette soirée ?
2° Peut-il y avoir dix-neuf invités ?
3° Peut-on avoir n'importe quel nombre d'invités
au-delà d'un certain minimum ?
-Si oui pourquoi ?
-Sinon indiquer les nombres possibles.
SOLUTION
1°
Le
plus petit nombre de personnes, possible est six.
-En
effet, de façon évidente, trois ou moins de trois
n'est pas possible.
-Quatre n'est pas possible car si trois
personnes serrent la main des trois autres, le quatrième
aura obligatoirement serré la main des trois autres.
-Cinq n'est pas possible, en effet chacun des quatre invités
donnant trois poignées de mains, le cinquième
en donnera ou zéro ou deux. |
|
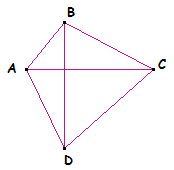
Six
est possible.
Nommons les invités A, B, C, D, E et F.
Voici une configuration possible des poignées de mains
:
A <-> B
B <-> C
C <-> D
D <-> E
E <-> F
A <-> C
A <-> E
B <-> D
Dans
ce cas, F échange une seule poignée de mains
avec E. |

|
2°
Il
ne peut y avoir dix-neuf invités car le nombre de personnes
doit être pair.
En effet, chaque fois qu'un invité X échange une poignée
de mains avec Y, alors Y échange une poignée de mains
avec lui. Le nombre de poignées de mains augmente donc de deux
et non pas de un.
Le nombre de poignées de mains est pair car échangé
entre deux personnes, donc compté deux fois.
Si les invités étaient au nombre de dix-neuf, le nombre
total de poignées de mains échangées serait de
18*3 +1 = 55.
C'est impossible car 55 est impair.
De façon génrale s'il y a (2n+1) personnes
(nombre impair), le nombre de poignées de mains est 2n
*3 +1 = 6*n +1.
Et 6*n + 1 est imapir d'où impossibilité dans
le cas général.
3° A
partir de six, tout nombre multiple de quatre fonctionne.
Huit
fonctionne
Choisissons les invités : A, B, C, D, E, F, G, H :
A <-> B
B <-> C
C <-> D
D <-> E
E <-> F
F <-> G
G<-> H
A <-> C
A <-> E
B <-> G
D <-> F
Et
chaque groupe, de quatre invités, supplémentaire peut
fonctionner en circuit fermé :
par exemple, chaque personne de ce dernier groupe ne donne une poignée
de mains qu'à une personne de ce groupe de quatre.
Ainsi tous donnent trois poignées de mains sauf l'une des personnes
du premier groupe de six ( Voir le premier schéma de la question
1° ), il s'agit de l'invité nommé
H.



