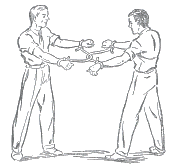
Détachez-les ! (1)
Deux amis A et B sont attachés l'un à l'autre comme indiqué sur le dessin.
L'extrémité d'une corde est fixée au poignet droit de A l'autre extrémité à son poignet gauche.
Une deuxième corde est passée dans la première, et ses extrémités sont fixées aux poignets de B.
Comment A et B peuvent-ils se libérer sans couper une corde ?Pouvez-vous les aider ?
SOLUTION
Je l'ai réalisé et photographié ICI...
Quelle que soit la gymnastique à laquelle ils se livreront autour de leurs cordes, ils n'y parviendront pas, mais la solution est simple.
B forme une petite boucle vers le milieu de sa propre corde, la glisse sous l'anneau de corde qui entoure le poignet droit de A
à la face interne du poignet et dans la direction allant du coude à la main et la passe autour de la main de A.
Il la glisse alors de nouveau sous l'anneau de corde qui entoure le poignet de A cette fois à la face externe du poignet et
dans la direction allant de la main au coude et, MAGIQUE ! les deux cordes se séparent.
(1) Fantaisies et Paradoxes mathématiques E.P.Northrop Dunod 1956
