Le problème avec Diophante.fr

On considère
- une pyramide à base carrée, dont les quatre faces sont des triangles équilatéraux ;
- un tétraèdre régulier dont les quatre faces sont des triangles équilatéraux.



Tous les triangles équilatéraux ont pour côté l'unité.
On accole la pyramide et le tétraèdre de sorte qu'une face de la pyramide coïncide avec une face du tétraèdre.
Quel est le nombre de faces du polyèdre résultant ?


Les deux animations qui suivent montrent la pyramide et le tétraèdre qui seront accolés l'un à l'autre.

Dans chacune des animations de cette page, nous pouvons toujours
- déplacer les solides avec la souris
ou bien
- avec le clavier en utilisant les touches fléchées ou les touches CRTL et Maj (Shift).
Le bouton STOPPER arrête l'animation (on peut toujours contrôler manuellement).
Le bouton AUTO relance l'animation automatique.

 

CLIQUER

 

 

CLIQUER

SOLUTION

REPONSE instantanée

On pense a priori que le solide est constitué de 5+4-2 = 7 faces.

Dans l'animation ci-dessous, modifier la hauteur du tétraèdre avec le bouton adéquat.
Observer, en haut de l'animation, le nombre de faces du nouveau solide.

CLIQUER

On peut voir les deux solides accolés en un seul polyèdre de cinq ou sept faces selon la hauteur du tétraèdre
(selon que le tétraèdre est régulier ou non).



REPONSE correcte

dans le cas d'un tétraèdre régulier

Dans cette animation, cliquer les flèches pour avancer ou bien reculer étape par étape.




CLIQUER

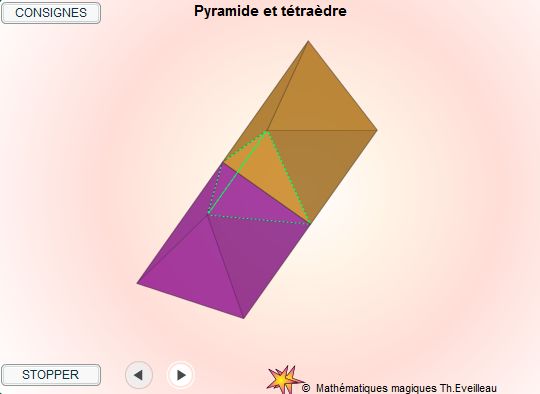
Finalement, le solide n'a pas sept faces mais seulement cinq.

En effet, par deux fois, une face de la pyramide se situe dans le même plan que celle du tétraèdre.
Et à chaque fois ces faces ont une arête commune. Cela constitue donc une seule face.

Le nouveau polyèdre a 5 faces.

 

---