Le tir au but, quelle est la meilleure position sur une ligne imposée ? Quelle sera la meilleure position pour tirer dans le but sur la ligne verte horizontale ? Prévoir la position du tireur en fonction de la largeur du but et de la position L de la ligne du tir. Les points B, L et C sont déplaçables à la SOURIS ou au CLAVIER pour plus de précision. EXPÈRIMENTONS Dans l'animation ci-dessous, un élément d'explication apparaît lorsqu'on obtient la meilleure position. ATTENTION, il faut déplacer le ballon très très lentement. La marge est très faible pour déterminer le bon angle. Je recommande de commencer le déplacement avec la souris. Un petit Bip sonore est entendu au passage de la bonne position. On peut la déterminer précisément en utilisant alors le clavier. Flèches GAUCHE et DROITE pour le Ballon. Flèches HAUT et BAS pour les points L et C.   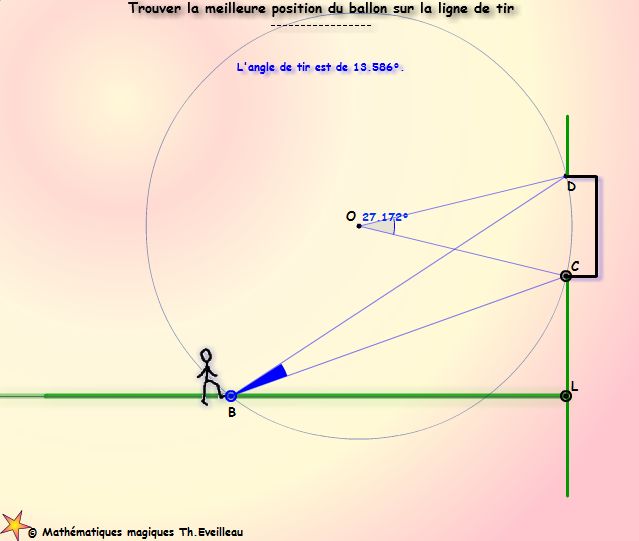CLIQUER     SOLUTION et EXPLICATION Dans l'animation suivante, nous allons essayer de COMPRENDRE la solution en analysant le cercle circonscrit aux deux points C et D poteaux du but et au ballon B. Comme précédemment, je recommande de commencer le déplacement avec la souris. Un petit Bip sonore est entendu au passage de la bonne position. On peut la déterminer précisément en utilisant alors le clavier. Flèches GAUCHE et DROITE pour le Ballon. Flèches HAUT et BAS pour les points L et C. CLIQUER     L'angle de visée en B varie dans le même sens que l'angle au centre en O. En effet la mesure de l'angle au centre inscrivant l'arc CD est égale au double de celle de l'angle inscrit en B interceptant ce même arc CD.. Cet angle au centre est d'autant plus grand que le rayon du cercle est plus petit, car l'arc intercepté est sous tendu par une corde de longueur constante. La distance la plus courte du point O à la droitre (BL), est obtenue en menant la perpendiculaire de O à cette droite ligne de tir. Le rayon OB le plus court, sera donc perpendiculaire à BL. Le rayon du cercle est le plus petit possible quand ce cercle est finalement tangent à la ligne de déplacement où se trouve le ballon. Nous obtenons ainsi la position optimale du ballon. Si le point I est le milieu de [CD], Nous avons alors R = OB = IL. Avec le théorème de Pythagore utilisé dans le triangle OCI rectangle en I, nous obtenons : R² = CO² = CI ² + OI ² . Nous avons BL=OI et BO = IL (rectangle BLIO). D'où IL² = BO ² = CO² = CI ² + BL² Nous retenons : IL² = CI ² + BL² . Finalement :   BL² = IL² - CI² La distance à choisir pour lancer le ballon est imposée par la largeur du but et la distance de la ligne de tir à ce but. ;) Les meilleurs joueurs de rugby font-ils ce calcul ?