La devinette

Quel peut être le lien mathématique entre un certain carré magique, la ville de Toronto un poème et un simple mot ?


Voici :
.Le carré magique cinq sur cinq de somme 65 construit avec les 25 premiers entiers naturels par un américain nommé Lobeck :

17	24	1	8	15
23	5	7	14	16
4	6	13	20	22
10	12	19	21	3
11	18	25	2	9

  .La station de métro Downsview de Toronto :


.Un poème écrit en vers libres en espagnol (il vient d'Argentine) :
"Fue y cayó. Y queda solamente la inútil cifra con pocos destinos poderosos,
tristes devenires sin el más sencillo bien. Idiota,
re idiota, sabe que sus encantos son ya latosos decimales.
Pobre..."
.Un mot :
CADAEIC

Qu'est-ce donc ?

SOLUTION et EXPLICATION

Le lien est le nombre Pi noté π :
.Le carré magique cinq sur cinq de somme 65 construit avec les 25 premiers entiers naturels par un américain nommé Lobeck :

17 24 1 8 15 23 5 7 14 16 4 6 13 20 22 10 12 19 21 3 11 18 25 2 9

Ce carré magique a bien entendu la particularité d'avoir - les cinq lignes, - les cinq colonnes et - les deux diagonales de même somme 65. Mais il y a mieux encore : π= 3,141 592 653 589 793 238 462 643 383 279... Remplaçons chaque nombre du premier carré par le chiffre de π situé à la position indiquée par ce nombre en partant de 3 (de rang 1).

2 4 3 6 9 6 5 2 7 3 1 9 9 4 2 3 8 8 6 4 5 3 3 1 5

Ainsi 17 est remplacé par 2 ; 1 est remplacé par 3 ; 2 est remplacé par 1 et ainsi de suite.
Nous obtenons le carré de droite. Il n'est pas magique MAIS...

Effectuons les sommes sur chaque ligne : 24, 23, 25, 29 et 17.
Nous les retrouvons sur les colonnes : 17, 29, 25, 24 et 23.
Certes elles sont dans un ordre différent mais tout de même c'est très surprenant.

POURQUOI ? Eh bien... on ne le sait pas !
Bien des choses sont encore à découvrir sur π nombre transcendant aux décimales infinies.

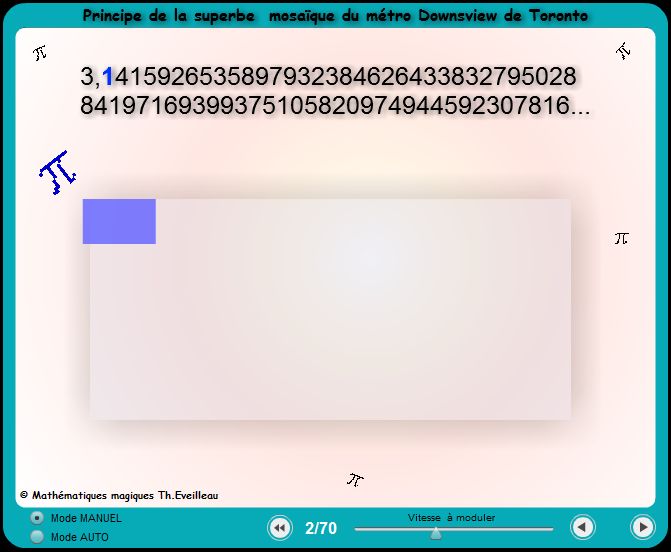
  .La station de Downsview
Le pavage de la mosaïque gigantesque de cette station est obtenu avec des rectangles dont la disposition paraît aléatoire.
Ce n'est pas le cas, elle est élaborée à partir des décimales du nombre π par Arlene Stamp (1993).
Elle utilisa ces "chiffres imprévisibles parce que le cercle et les murs courbes étaient une caractéristique de conception de cette station".
Avantage supplémentaire : la réalisation était assez économique.

Les rectangles colorés sont tous de même taille, mais ils se superposent de manière à ce que les parties qui se chevauchent soient proportionnelles à la décimale correspondante du nombre π.
Cela commence à 1 puis 4 puis 1 puis 5 et ainsi de suite.

Comme les décimales de π paraissent aléatoires l'ordre utilisé paraît désordonné...

L'animation ci-dessous simule un tel pavage où les dalles se superposent sur des parties proportionnelles
aux décimales de Pi.

CLIQUER

.
.Un poème écrit en vers libres en espagnol (il vient d'Argentine) :
Ce poème fait partie de la très longue liste des nombreuses odes et autres hommages rendus à π.
Il s'agit de pi-philologie : méthode mnémotechnique basée sur l'usage de poèmes ou de textes pour se rappeler les décimales de e π.
Chaque mot représente un chiffre de π, correspondant au nombre de lettres du mot.
Ainsi
Fue donne le chiffre 3
y donne le chiffre 1
cayó donne le chiffre 4
et ainsi de suite.

Certaines astuces faisant appel à des mots de plus de 9 lettres sont uilisées à chaque fois qu'apparaît un zéro...

.Un mot : CADAEIC
Dans ce mot, chaque lettre doit être remplacée par son rang dans l'alphabet.

C -- > 3
A -- > 1
D --> 4
A --> 1
E --> 5
I --> 9
C --> 3
On peut ainsi noter qu'il s'agit d'une approximation : le dernier chiffre devrait être 2 qui serait suivi de 6.
L'expression correspond donc à un arrondi.

CADAEIC vient de Cadaeic Cadenza, œuvre de Keith dont le but est d'emmagasiner 3834 décimales de π.

.Et maintenant je suis certaine que chacun devinera aisément ce qui se cache dans ce poster

( des éditions du Kangourou des mathématiques).

Réponse

Ce sont les décimales de π.
Chaque bande de couleur a une alrgeur proportionnelle à chaque décimale de ce nombre.
La première bande représente 3.

3,1415926535897...