 
Un
jour Bacchus ayant vu que Silène
Dormait
profondément, prit sa coupe, et sans gêne,
Dans
le cellier, à l'aise il s'attabla,
Près
d'une amphore pleine
Où
reposait un vieux vin, qu'avec peine
Son
ami conservait pour des jours de gala.
Il
but pendant le triple du dixième
Du
temps qu'à boire seul Silène eût employé
Pour
vider l'amphore elle-même ;
Mais
Silène survient, et son chagrin extrême
Dans
le reste du vin est aussitôt noyé.
Quand
l'amphore fut vide,
Avec
regret Bacchus vit que sa part
Du
précieux liquide
N'avait
été que tout juste le quart
De
celle de Silène.
Si,
tout d'abord, d'une commune haleine,
Chacun
buvant à sa façon,
Ils
s'étaient réunis, ils auraient mis, dit-on,
Huit
quarts d'heure de moins pour épuiser l'amphore.
Comment
l'a-t-on su ? Je l'ignore.
On
veut, d'après cela, trouver exactement
Le
temps que chacun d'eux eût mis séparément,
Si,
buvant seul, de la même manière,
Il
avait mis à sec l'amphore tout entière.
|
|
Source
: Problèmes plaisants et délectables
par Claude-Gaspar Bachet sieur de méziriac
ed de Paris : Gauthier-Villars, 1874
|
 Solution
 
Solution
|
|
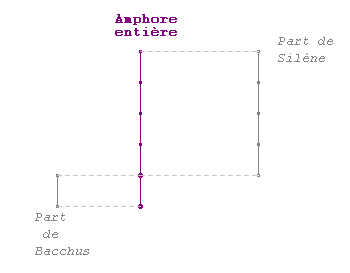
Avec
regret Bacchus vit que sa part
Du
précieux liquide
N'avait
été que tout juste le quart
De
celle de Silène. |
Bacchus
a donc bu 1/5 ème de l'amphore
et
Silène a bu 4/5ème de
l'amphore. |
|
|
|
|
Il
but pendant le triple du dixième
Du
temps qu'à boire seul Silène eût
employé
Pour
vider l'amphore elle-même ; |
|
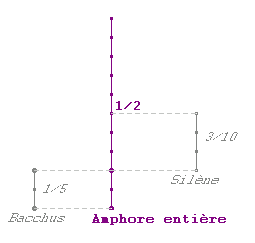
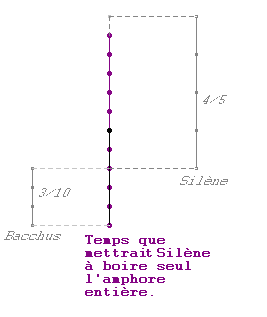
Donc
Bacchus
a bu 1/5 ème de l'amphore
pendant 3/10ème du temps que
mettrai Silène pour vider l'amphore.
Pendant ce temps Silène aurait bu 3/10 ème
de l'amphore entière. |
|
Pendant
ce même temps ,
à eux deux ensemble, ils auraient bu
(1/5 + 3/10 = 5/10) ème de l'amphore.
Or 5/10
= 1/2
A eux
deux ils auraient donc bu la moitié
de l'amphore.
|
|
|
|
|
Si,
tout d'abord, d'une commune haleine,
Chacun
buvant à sa façon,
Ils
s'étaient réunis, ils auraient mis
|
Pour épuiser
l'amphore, ils auraient mis le double du temps précédent
soit
6/10 ème
du temps
que mettrai Silène pour vider l'amphore.
|
|
| En
réalité , |
|
Silène a bu 4/5ème
de l'amphore, il a donc mis
4/5 ème du temps
qu'il aurait mis pour vider seul l'amphore.
A eux d'eux, ils ont mis
(3/10 + 4/5) ème soit
11/10
ème du temps que mettrait Silène
pour vider seul l'amphore.
|
|
|
|
|
Si,
tout d'abord, d'une commune haleine,
Chacun
buvant à sa façon,
Ils
s'étaient réunis, ils auraient mis, dit-on,
Huit
quarts d'heure de moins pour épuiser l'amphore.
|
La
différence entre 11/10
ème et 6/10
ème
du temps que mettrait Silène pour vider l'amphore
est de 2 heures. Or (11/10 - 6/10) = 5/10 = 1/2.
La
moitiédu temps que mettrait Silène pour vider
l'amphore est donc de 2 heures.
Silène mettrait
donc 4
heures pour vider
seul l'amphore.
Bacchus a bu 1/5
ème de l'amphore pendant 3/10
ème
de 4 heures,
soit pendant 1,2 heure.
Pour boire l'amphore entière, il mettra 5 fois plus de
temps.
Bacchus mettrait
6 heures, pour boire l'amphore entière.
|
Voici
quelques réponses en vers proposées par Fred.
En
buvant tout sons soûl, c'est en quatre heures à peine,
Que fut retrouvé saoul le malheureux Silène.
Mais en moitié de plus, le plus prudent Bacchus
A fini lui aussi par être ... sur le cul !
Une
autre
Bacchus
mit moitié plus, et en fut ... sur le cul.
Temps de l'un et de l'autre, faites un peu le calcul,
Et dix heures tout rond vous trouverez sans peine.
Enfin
une dernère
C'est,
buvant tout son soûl, que le pauvre Silène
S'était retrouvé saoul au bout d'un certain temps.
C'est, se croyant plus sage, que le divin Bacchus
Prit pour le même ouvrage encore moitié autant.
Ces deux temps assemblés, que vous trouvez sans peine,
C'est dix heures tout rond ! à tomber ... sur le cul !
|