On m'assura que Sésostris avait partagé l'Egypte entre tous ses sujets, et qu'il avait donné à chacun une égale portion de terre en carré. Hérodote

Origines connues de la géométrie Géométrie  grecque Des grecs jusqu'à nos jours Des racines qui donnent des ailes : pour les enfants

  Origines connues de la géométrie

• Les premières recherches connues de la géométrie sont dues aux Egyptiens et aux Babylonniens (2000 ans avant notre ère).
  

  Les inondations périodiques du Nil obligeaient les arpenteurs égyptiens à refaire chaque année le tracé des propriétés. Les formules utilisées étaient empiriques : Ainsi l'aire d'un quadrilatère de côtés a, b, c, d était donnée par (a + c)/2 x (d + b)/2 Ce dernier résultat n'est en fait qu'une approximation. La formule devient exacte pour un rectangle. De même l'aire d'un triangle isocèle de côtés a, a, b était donnée par (a x b)/2. Formule qui est fausse dans tous les cas mais devient une assez bonne approximation si le triangle isocèle a un angle très aigu.

  Ces informations proviennent d'un papyrus, appelé papyrus de Rhind (manuel de calcul du scribe Ahmès) qui a été daté de 1700 à 2000 ans avant notre ère.
• On a cependant constaté que les Egyptiens connaissaient le volume du tronc de pyramide et la surface de la sphère.
  On a aussi retrouvé sur des tablettes babylonniennes (2000 avant notre ère) une série de problèmes se ramenant à la résolution d'équations du second degré et même d'équations bicarrées.

  Géométrie  grecque

Les connaissances mathématiques des Egyptiens et des peuples orientaux parvinrent en Grèce à la faveur d'échanges commerciaux.

La tradition attribue à Thalès (600 ans avant notre ère) l'introduction en Grèce de la géométrie égyptienne. Thalès fut un précurseur surtout préoccupé de problèmes pratiques (calcul de hauteurs de monuments à l'aide d'un bâton et de la proportionnalité des ombres). La géométrie grecque qui fut une réussite éclatante de la science humaine en faisant preuve d'une ingéniosité exceptionnelle, fut marquée par deux Ecoles : celle de Pythagore et celle d'Euclide.

 

• Géométrie Pythagoricienne : Ecole de Crotone
  

  Pythagore fut un philosophe grec né à Samos vers 580 avant notre ère et mort vers 500 avant notre ère. Il voyagea en Egypte et s'installa à Crotone en Italie où il fonda une école célèbre. Nous devons à l'école de Crotone une nouvelle démarche dans la recherche géométrique.

  
  A cette époque les concepts de point, ligne et surface étaient particuliers :
  • Le point n'était pas le point sans dimension, c'était un être concret, appelé monade, matérialisé par un grain de sable.
  • La ligne était alors une succession de monades dont le nombre donnait la mesure.
  • Toutes les longueurs étaient donc commensurables.

   Le théorème de Pythagore devait ruiner la géométrie construite sur le concept de monade.
  En effet si on considère un triangle rectangle isocèle dont le rapport de l'hypoténuse sur le côté de l'angle droit est m/n tel que m et n soient premiers entre eux, le théorème permet d'établir :
  m² = 2 n² d'où l'on tire que m est pair (*1)
  Soit m² est un multiple de 4
  ainsi n² est pair
  donc n est pair!
  ce qui est contraire à l'hypothèse que m et n sont premiers entre eux.
  Le fait de s'apercevoir qu'il existait des longueurs incommensurables modifia fondamentalement la géométrie de l'époque. (*2) 

 

• Géométrie Euclidienne : Ecole d'Alexandrie
  

  Fondée en 331 avant notre ère par Alexandre le Grand, la ville d'Alexandrie devint rapidement sous la protection des Ptolémées, le centre intellectuel du monde antique. Les mathématiques y furent particulièrement travaillées et la célèbre Ecole mathématicienne d'Alexandrie connut trois représentants exceptionnels : Euclide, Archimède et Appolonius.

  Les travaux de cette école débouchèrent sur une œuvre qui pendant plus de 20 siècles servit de base à toute étude géométrique : les Eléments. Cette œuvre est composée de 15 livres dont 13 sont dus à Euclide (300 avant notre ère).
  Ces 13 livres traitent des figures géométriques, des polygones inscrits et circonscrits à un cercle et leurs propriétés, des proportions, de la similitude, de la géométrie dans l'espace ainsi que de la théorie des nombres et des incommensurables.
  
  Voici un exemple extrait des Eléments dans le livre I, proposition 43.
  Prenons un rectangle. Par un point quelconque de sa diagonale traçons les parallèles à ses côtés.
  
  Les deux rectangles de chaque côté de la diagonale ont la même aire.
  
  
• 
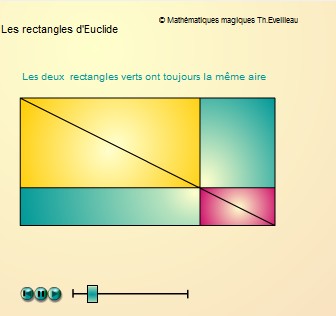
  Cliquer
  
  Le résultat est identique avec des parallélogrammes au lieu de rectangles.
  
  
• 
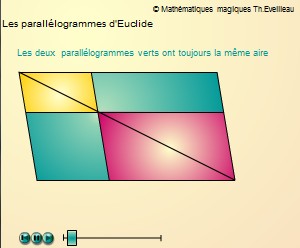  Cliquer
  

  
  Archimède (287-212 avant notre ère) compléta les Eléments par une étude très approfondie sur les cercles, les sphères et les cylindres... Il donna un encadrement du nombre PI :
  3 + 10/71 < Pi < 3 + 1/7 soit 3.1408 < Pi < 3.1428
  Avec l'étude des coniques par Appolonius (200 avant notre ère) nous avons l'ensemble de la géométrie élémentaire telle qu'elle était enseignée il y a quelques années. (*3)

 

Des grecs jusqu'à nos jours

La décadence grecque coïncide avec une longue période de temps obscurs pour les mathématiques en général
et la géométrie en particulier... jusqu'au XV^ème siècle début de la Renaissance.
Nous pouvons, dans cette longue période d'immobilisme et presque de régression scientifique retenir deux facteurs :

• La civilisation romaine qui fit suite à la civilisation grecque était toute portée vers la conquête militaire, l'administration civile, l'acquisition de richesses et la construction de monuments gigantesques, cela au détriment de la science et de l'humanisme... En 529 (après J.C) l'Empereur romain Justinien, par sanction d'un enseignement païen fit fermer les écoles d'Athènes.
• La grande bibliothèque d'Alexandrie brula à plusieurs reprises. (*4)
  En raison de l'unicité, du nombre et de la richesse des ouvrages disparus, cela représente une perte considérable pour l'humanité.

Jusqu'au XIIIème siècle seuls les Arabes et les Hindous empêchèrent la régression scientifique de prendre une ampleur qui aurait fait sombrer dans l'oubli les merveilleux travaux des Grecs. Dans cette période, en effet ce sont les savants de culture arabe qui sont les héritiers de la Grèce et les promoteurs de la connaissance. Ce sont eux dont les œuvres, une fois traduites en latin, vont déclencher en Occident le grand mouvement de pensée qui aboutit au brillant essor du XIIIe siècle. Dès lors, ce sont les philosophes et les chercheurs des pays de chrétienté, qui prennent l'initiative.

Avec la Renaissance et l'invention des presses d'imprimerie débuta une période d'intense activité pour le développement des sciences en général et des mathématiques en particulier. Cette activité se poursuit jusqu'à nos jours parfois ralentie par les guerres et les invasions.

Jusqu'au XVII^ème siècle on admettait en gros que la géométrie s'occupait des figures de l'espace et que l'algèbre s'intéressait aux nombres.

En 1637 Descartes associa ces deux notions en créant le concept de repère. La géométrie analytique était née ! Elle apporta une richesse nouvelle aux mathématiques en contribuant entre autres aux théories de Newton et Leibniz pour aboutir à celle de la relativité d'Einstein.

Cantor, Hilbert, Galois ainsi que bien d'autres apportèrent enfin aux mathématiques une assise différente au XIXème siècle, créant une nouvelle pensée, un nouvel éclairage, dont les retombées de nos jours sont connues sous le nom de Mathématiques Modernes...

Aujourd'hui, la géométrie fait souvent peur aux étudiants. Pourtant elle procure des démonstrations magnifiques et élémentaires. Dans "Richard Feynman le mouvement des planètes autour du soleil " les auteurs David Goodstein et Judith Goodstein reconstruisent pas à pas la démonstration radicalement élémentaire que Richard Feynman exposa le 13 mars 1964 au cours d'une "Guest lecture" à Caltech. Page 155 de cet ouvrage, les auteurs retranscrivent le plaisir qu'éprouva Feynman en réalisant une telle démonstration alors qu'il aurait pu utiliser des outils plus modernes et efficaces mais beaucoup moins élémentaires : "...pour importe la démonstration géométrique, il faut beaucoup d'ingéniosité. Mais une fois présenté, c'est simple et élégant. Je veux dire c'est fini, c'est tout. ... C'est très difficile, mais l'élégance des démonstrations une fois que les découvertes sont faites est vraiment magnifique. La puissance de la méthode analytique, c'est qu'il est beaucoup plus facile de découvrir les choses que de les démontrer. Mais sans aucune élégance. Cà gâche beaucoup de papier, avec des x et des y et des simplifications et tout ce genre de choses... "

NOTES

(*0) Sources
La Science antique et médiévale sous la direction de RENE TATON 1957 éditions PUF
Civilisation grecque d'Euripide à Alexandre de André Bonnard 1991 éditions complexe

(*1) On doit à l'école de Crotone la démonstration :
"Si le carré d'un nombre a est pair, alors a est pair".
Soit (a² pair => a pair)

(*2) "Mesurer une grandeur, c'est lui associer un nombre exprimant son rapport à une autre de même espèce choisie pour unité"
MESURE = APPLICATION dans un ensemble de NOMBRES
m : a |----> m(a) telle que m(u) = 1 
Ce nombre est entier si la grandeur est multiple de l'unité; fractionnaire en cas de commensurabilité; irrationnel dans les autres cas"

(*3) Un des six axiomes fondamentaux des Eléments :
"Le tout est plus grand que la partie ".
Au niveau des cardinaux des ensembles la situation changera...
Galilée (début XVIIème siècle) remarque qu'il y a "autant" d'entiers pairs que d'entiers.
Ce paradoxe est utilisé par Dedekind et Cantor (1870) pour définir les ensembles infinis.

(*4) En 47 av. J.-C., au cours de la guerre civile entre Jules César et les partisans de Pompée, un incendie détruisit la flotte égyptienne et s'étendit à certains entrepôts de la bibliothèque, anéantissant quelques 40 000 volumes.
Selon la légende, la bibliothèque d'Alexandrie fut détruite par le feu à trois reprises :
            par l'empereur romain Aurélien en 272 av. J.-C.,
            par l'empereur Théodose Ier en 391
            et par le calife Omar Ier (v. 581-644) en 640.
(D'apès Encyclopédie Encarta 97)