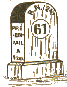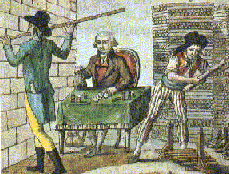LA MESURE       

    Exprimer les rapports de longueurs à l'aide de naturels

La notion de commune mesure
Considérons deux grandeurs inégales correspondant pour fixer les idées, à des objets longs, disons deux baguettes ; nous voulons les comparer ; la première idée qui vienne à l'esprit est de voir combien de fois la petite va dans la grande. Ou en d'autres termes, si la petite multipliée par un naturel n bien choisi n'est pas équivalente à la grande. Si on trouve un tel entier n, on dira que la petite va n fois dans la grande, ou qu'elles sont entre elles comme 1 est à n. On dit aussi que les deux grandeurs sont entre elles dans la proportion de 1 à n. Si par ailleurs la petite baguette ne va pas un nombre entier de fois dans la grande, une bonne idée est de chercher une troisième baguette qui irait un nombre entier m de fois dans la petite, et un nombre entier n de fois dans la grande. On a bien l'impression qu'il est toujours possible de trouver une troisième baguette qui ait cette propriété, quitte éventuellement à la choisir très petite… mais si on trouve une telle troisième baguette, alors on dira que la petite baguette de départ est à la grande comme m est à n. La troisième baguette ou plus précisément sa grandeur, est appelée commune mesure des deux autres. 

La méthode de coïncidence pour la commune mesure
Soit à chercher une commune mesure entre deux objets (ou deux grandeurs). Pour pratiquer la méthode dite de coïncidence, il faut disposer d'un nombre de copies des deux objets à comparer. On additionne d'une part les copies du premier objet, et d'autre part les copies du second, jusqu'à ce que (si cela est possible), les deux sommes soient équivalentes ; Par exemple, s'il s'agit de baguettes, on aligne des copies de la première et des copies de la seconde jusqu'à obtenir deux segments de même longueur. 

L'accident
Contrairement à ce que l'intuition pourrait faire croire, il arrive qu'il n'y ait pas de commune mesure pour deux grandeurs. Essayer de trouver une commune mesure entre le côté du carré et sa diagonale. En fait on y arrive presque… et on obtient sans calculette une jolie façon d'approcher le nombre racine de 2. 

 Les comparaisons de grandeurs dans la langue

On dit :

J'ai fait deux fois plus de chemin que lui

ce qui veut dire curieusement la même chose que :

J'ai fait deux fois autant de chemin que lui
J'ai fait trois fois plus de chemin que lui
Cette corde est trois fois plus grande, ou trois fois plus petite que celle-là .

Les termes demi, moitié, quart, etc. sont peu utilisés pour de telles comparaisons, c'est à dire pour exprimer qu'une grandeur est deux, trois, quatre… fois plus petite qu'une autre.
On ne dit guère :
J'ai fait un tiers de fois autant de chemin que lui .

Par contre on dit :

Ce sac est une fois et demie aussi lourd que cet autre.

 Une phrase telle que :
Ce sac est une fois et demie plus lourd que cet autre
serait ambiguë : on ne saurait pas si le poids du gros sac vaut 1,5 fois ou 2,5 fois le poids du petit.
Selon les circonstances, la langue commune exprime les rapports de diverses autres façons. Par exemple, on exprime la proportion d'un mélange en disant :
deux parties d'eau pour trois parties d'alcool
On recourt au rapport lui-même :
Les distances sur la carte sont à celles sur le terrain dans le rapport de 1 à 50 000 .
Dans un langage un peu plus savant, hérité sans doute de la géométrie ancienne on dit aussi :
telle grandeur est à telle autre comme 2 est à 9 .
Mentionnons l'expression d'un rapport entre deux types d'objets dans un ensemble discret, éventuellement infini :
Un homme sur trois est fumeur
Dans un tel pavage, un triangle sur trois est noir  

Nous avons observé qu'il existait parfois une commune mesure pour deux grandeurs de même nature. L'existence d'une commune mesure est bien commode puisqu'elle ramène la comparaison de deux grandeurs à la comparaison de deux nombres naturels. Mais elle a pour inconvénients d'une part de ne pas toujours exister, et d'autre part de ne s'appliquer aisément qu'à deux grandeurs isolées. En effet, il devient vite très difficile de comparer entre elles trois, quatre,… cent grandeurs en cherchant des communes mesures.

D'où l'idée de choisir au départ une grandeur de référence appelée unité de mesure, à laquelle on comparera toutes les autres grandeurs de même nature. L'inconvénient c'est que l'unité n'est généralement pas contenue un nombre entier de fois dans une grandeur quelconque à mesurer, et qu'il y a un reste. Celui-ci est exprimé quand c'est possible par une fraction de l'unité. Or les fractions sont des objets mathématiques encombrants, soumis à des règles de calcul plus nombreuses et plus compliquées que les entiers naturels.
A cette étape une remarque d'ordre pratique s'impose ; choisir au départ une unité de mesure constitue certes un grand progrès, mais laisse la question du choix de cette unité. Une unité de poids commode pour un pharmacien ne l'est pas pour un sidérurgiste ; une unité de longueur commode pour un astronome ne l'est pas pour un menuisier. C'est pour cela qu'on a vu apparaître très tôt dans l'histoire la pratique des unités emboîtées.

Les systèmes anglais d'unités en fournissent de bons exemples ; Considérons donc les mesures anglaises de longueurs, que voici dans l'ordre croissant :

le pouce (inch) vaut 2,54 cm et est subdivisé en seizièmes ; le pied (foot) vaut 12 pouces ; le yard (yard) vaut 3 pieds ; la toise (fathom, unité utilisée pour les sondes sur les cartes       marines anglaises, appelée brasse) vaut environ 2 yards ; la chaîne d'arpenteur (chain) vaut 22 yards ; le furlong (furlong) vaut 10 chaînes ; le mille (mile) vaut 1760 yards ou 80 chaînes.

Convertisseur de longueurs CLIQUER.

L'inconvénient d'un tel système est que les rapports entre unités successives n'obéissent à aucune règle claire et en particulier ne sont aucunement coordonnés au système de numération décimal. D'où l'obligation de manipuler des fractions chaque fois que se pose un problème de conversion d'unités. Et comme il faut être plus instruit pour calculer avec des fractions qu'avec des décimaux, un tel système d'unités est peu démocratique. Il est tout à fait étonnant qu'il ne soit pas en voie de liquidation aux Etats-Unis et en Angleterre, deux siècles après l'adoption du système décimal de mesures par un grand nombre d'autres nations.

Occupons nous de ce système :
Soit à mesurer un poteau dans le système décimal ; On commence par déterminer le nombre de fois que le mètre est contenu dans le poteau disons 12 fois. Supposons qu'il reste un bout inférieur à un mètre ; On cherche le nombre de fois que le décimètre est contenu dans ce reste : ce nombre est compris entre 0 et 9, disons 7. On continue de même avec le centimètre , puis le millimètre etc.
Ou bien un tel processus de mesure s'arrête de lui même après un nombre fini d'étapes,ou bien il se prolonge sans cesse. Dans tous les cas pratiques, on l'arrête soit lorsqu'on atteint une précision suffisante pour ce qu'on veut faire de la mesure, soit lorsqu'on est plus capable de discerner les sous-unités parce qu'elles sont devenues trop petites. Il est important toutefois de savoir que sur un plan théorique, le processus de mesure peut ne jamais s'arrêter. On obtient alors des mesures qui, s'expriment par une suite infinie de résultats.
D'où des phénomènes mathématiques nouveaux…les nombres périodiques avec des chiffres qui se répètent indéfiniment : 6/11 = 0,54545454…
ou
0,999…. = 1 . ( Mais oui! )

Jusqu'au XVIe siècle, les rationnels non entiers étaient écrits sous forme de fractions s'ils étaient plus petits que un, et en juxtaposant leur partie entière écrite en numération décimale et une fraction dans le cas contraire.

Exemple : 42,375 s'écrivait 42 3/8.

Les calculs de fractions compliqués n'étaient pas à la portée de tout le monde et s'ajoutaient aux difficultés ordinaires de l'artisanat et du commerce.  

La Disme de Stevin  

Simon Stevin né à Bruges en 1548 et mort à La Haye en 1620, grand ingénieur et mathématicien a proposé en 1585 de privilégier les fractions décimales et d'écrire les rationnels non entiers sous une forme proche de nos nombres à virgule
L'avantage décisif de cette représentation des nombres est qu'elle élimine les encombrants calculs de fractions et ramène les règles des opérations de l'arithmétique à celles que l'on connaît pour les nombres naturels, à ceci près qu'il faut apprendre à placer correctement la virgule.

La proposition de Stévin est parue en 1585 sous forme d'un opuscule intitulé en flamand Thiende et immédiatement traduit en français sous le titre La Disme. le succès de la Disme a été considérable et la pratique du calcul en décimal s'est répandue à travers l'Europe en une dizaine d'années.

 L'évolution du système de mesures a été beaucoup plus lente, les unités anciennes et locales et incohérentes ayant résisté jusqu'au dix-neuvième siècle et même jusqu'à nos jours dans les pays anglo-saxon..

  La promulgation des mesures décimales

C'est à la fin du Siècle des Lumières que fut mise en œuvre, par la Révolution française, l'idée d'un système de mesures fondé scientifiquement et destiné à remplacer toutes les mesures anciennes.

Le litre, le gramme, le mètre.

Les calculs étaient compliqués et les erreurs fréquentes. La confusion régnante favorisait les fraudes, ce dont le petit peuple pâtissait (particulièrement à l'époque des famines qui ont accompagné la Révolution).

Sur la proposition de Talleyrand, l'Assemblée Nationale décide dès 1790 la constitution d'un système unifié de poids et mesures, entreprise qui s'étalera sur une dizaine d'années. L'étude en est confiée, dans l'Académie des Sciences, à une commission réunissant des savants réputés : Borda, Lagrange, Lavoisier, Tillet et Condorcet, et plus tard Laplace et Monge.

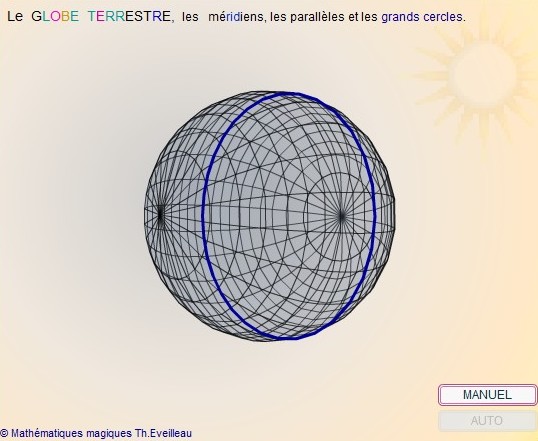
Le point de départ était l'unité de longueur. Elle fut définie comme la dix-millionnième partie du quart du méridien terrestre.
La difficulté majeure a été de mesurer ce méridien (ou au moins un arc de méridien assez long pour obtenir une grande précision), travail de plusieurs années qui fut confié à Delambre et Méchain et aboutit à la fabrication d'un mètre étalon (Cf Eratostene).

En 1795, le 18 germinal an III du calendrier républicain, toutes les unités de mesure de longueur sont remplacées par le mètre, ses multiples et ses sous-multiples.

L'are, le franc, le stère.

En 1840, l'utilisation du système métrique est obligatoire et notre système de calcul décimal est imposé dans les écoles. A partir du mètre les scientifiques ont défini le système métrique, il permet de mesurer :

Des longueurs : l'unité principale est le mètre. Des surfaces : l'unité principale est le mètre carré, aire d'un carré d'un mètre de côté. Des volumes : l'unité principale est le mètre cube, volume d'un cube d'un mètre de côté. Des capacités : l'unité principale est le litre.

Convertisseur volumes capacités CLIQUER.

 Au cours des XIXe et XXe siècles, des systèmes d'unités et des étalons améliorés ont été mis au point et promulgués par des Conférences et Conventions Internationales, quoique sans remise en cause du système décimal.
L'unité de poids (la notion de masse n'est pas utilisée dans les documents officiels de l'époque) est dérivée de l'unité de longueur : le kilogramme, adopté en 1799, est défini comme le poids d'un décimètre cube d'eau distillée à 4° centigrade.

 Les unités de temps et d'angle ne sont pas comprises dans ce mouvement de réforme, puisque la nature fournit pour ces grandeurs des étalons toujours aisément disponibles : pour le temps le jour solaire divisé en 86400 secondes, et pour les angles le tour entier, le demi-tour et l'angle droit. les subdivisions décimales de ces dernières unités n'ont par ailleurs pas suscité beaucoup d'intérêt. 

L'histoire du mètre

Sans mesure, il n'est pas de science possible. L'étalon de longueur est sans doute la mesure la plus connue, la plus utile; En différentes contrées, on employa autrefois la toise, le pied, le pouce, la ligne, la brasse, la coudée, etc. Selon les lieux, un même mot représentait souvent des mesures différentes et il en résulta une grande confusion. Des projets d'unification apparurent sous Philippe le bel, Louis XI, François Ier et Louis XIV, mais sans succès.

Il fallait d'abord s'entendre sur l'unité de longueur. Notre bon vieux mètre connut des fluctuations. Après que Picard, en 1670, eût proposé la longueur du pendule qui bat la seconde sexagésimale, on en vint (La Condamine en 1766) à prendre la mesure d'un degré de méridien au Pérou. En 1790, Talleyrand proposa le retour au pendule qui bat la seconde à la latitude de 45° au niveau de la mer. Puis la loi du 26 mars 1791 revint à la mesure du méridien et adopta le mot " mètre " pour désigner la dix-millionnième partie de la distance de l'équateur au pôle. Le décret du Ier août 1793 fixa la longueur de ce mètre à 3 pieds 11 lignes et 44 centièmes.

La loi du 7 avril 1795 institua le système métrique décimal, création française qui sera adoptée en Europe d'abord puis dans la plupart des Etats du monde. De février 1796 à décembre 1797, la Convention fit placer dans Paris seize mètres-étalons gravés dans du marbre pour familiariser la population avec la nouvelle mesure. Il n'en subsiste que deux : l'un est au 36 de la rue de Vaugirard, à droite de l'entrée ; l'autre, replacé en 1848, est au 13 de la place Vendôme, à gauche de l'entrée du ministère de la Justice. 

CLIQUER chaqque image pour l'obtenir en PLEIN ECRAN

Mètre étalon 13 place Vendôme Paris Mètre étalon 36 Rue Vaugirard Paris Mètre étalon Place Nationale Montauban

Le 22 juin 1799, une commission amena le mètre à 3 pieds 11 lignes et 296 millièmes ; une règle de platine à mesurer de bout en bout devint l'étalon officiel déposé aux Archives Nationales, puis transféré à Sèvres le 10 décembre. Il fallut arriver au Ier janvier 1840 pour que le système métrique fût officiellement adopté.
En 1872 fut créée la Convention internationale du mètre.

En 1889, la Ière Conférence Internationale des Poids et Mesures déposa un nouveau mètre-étalon au pavillon de Breteuil à Sèvres. C'est une barre en platine irridié (90% d'iridium) de plus d'un mètre de long, à section en X.

La longueur officielle du mètre est celle qui sépare, à la température de 0°C, deux traits fins a et b tracés dans le sillon central.

De cet étalon international, la France possède la copie N°8, déposée au Conservatoire des Arts et Métiers de Paris.

La 7ème Conférence des Poids et Mesures, réunie en 1927, observant que les étalons matériels étaient sujets à des déformations, fixa un étalon naturel de longueur comme témoin ; Elle détermina, à un dix-millionnième près, le rapport de la longueur du mètre à la longueur d'onde de la raie rouge du cadmium qui vaut (dans l'air sec et à 15°C sous une pression normale) 0,64384696 mm (1 millième de millimètre). 

Mais depuis 1945, on sait produire, grâce à la séparation des isotopes, des radiations optiques plus fines et plus simples que la raie rouge du cadmium ; ce qui nous valut une nouvelle définition en octobre 1960 lors de la 11ème Conférence Générale des Poids et Mesures à Paris : le mètre vaut 1650 763,73 longueurs d'onde, dans le vide, de la radiation correspondant à la transition entre les niveaux 2p10 et 5d5 de l'atome de krypton 86.

Le mètre n'est plus rattaché à un objet périssable mais à un phénomène physique immuable..
Améliorant encore la précision, la Conférence donna le 20 octobre 1983 une dernière définition du mètre (rendue possible par le laser, inconnu en 1960) : c'est la longueur du trajet parcouru dans le vide par la lumière en 1/299 792 458 ^ème de seconde.

Cette définition est donc liée à celle de la seconde définie en 1967 par une transition atomique :
la seconde est la durée de 9 192 631 770 périodes de la radiation correspondant à la transition entre les deux niveaux hyperfins de l'état fondamental de l'atome de césium 123.

CLIQUER

CF jour et la nuit avec le globe terrestre.

NICOLAS ROUCHE Le sens de la mesure ed Hatier
ANDRE. JOUETTE Le secret des nombres ed Albin Michel
ANNE-MARIE MARCHETTI Nombres & Formes ed du Choix
LOUIS MARQUET, ALBERT LE BOUCH, YVES ROUSSEL
Le système métrique, hier et aujourd'hui ed A.D.C.S 1996
A.MARIJON, R.MASSERON, E.DELAUNAY Arithmétique Géométrie ed Hatier 1947
Elem-Math VIII A.P.M.E.P (Association des Professeurs de Mathématiques de l'Enseignement Public) 1986
FLORENCE TRYSTRAM Le procès des étoiles Petite bibliothèque Payot/Voyageurs 1997
LAROUSSE Chronique de la révolution  ed Jacques legrand S.A., Paris 1989.