Les polygones d'Archimède L'étude du cercle amène Archimède à donner une approximation de π. Pour cela, il inscrit et circonscrit au cercle un polygone régulier de quatre-vingt-seize côtés, ce qui lui donne l'encadrement 3 + 10 / 71 < π< 3 + 1/ 7 A l'aide du théorème de Pythagore effectuons les calculs des périmètres des polygones réguliers inscrits. Dans le but d'obtenir les approximations de π on assimile la longueur du cercle avec celle du polygone inscrit. A chaque étape nous doublons le nombre de côtés. Choisissons n comme nombre d'étapes en partant de n=2. Nous ne considèrerons pas la valeur 1. Lorsque n=2 (2²=4) nous partons du carré, lorsque n=3 (23=8) nous obtenons un octogone, lorsque n=4 nous obtenons un polygone à 16 côtés (24=16).... Si le rayon du cercle est r alors le côté du carré mesure r . Calcul du côté C8 de l'octogone vert : De même pour passer du côté C8 de l'octogone au côté C16 du polygone ayant 16 côtés nous calculerons : et ainsi de suite... Pour chaque polygone de côté Cn le périmètre est 2n Cn. Le périmètre du cercle est 2π r. Plus le polygone a de côtés et plus son périmètre est proche de celui du cercle. En divisant 2n Cn par 2r on a l'approximation du nombre π à cette étape. C'est ce calcul qui est utilisé dans l'animation ci-dessous. Il suffit d'entrer le numéro (à 1 chiffre) de l'étape pour obtenir automatiquement l'approximation associée du nombre π et la figure correspondante. Un clic sur une touche quelconque relance la construction. Pour un autre résultat, il suffit d'effacer le nombre précédent avant d'en entrer un nouveau. PLEIN ECRAN   π aujourd'hui...  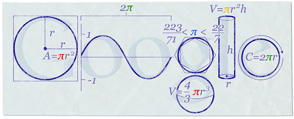Logo Google Piday