Lorsque les pièces d'un puzzle sont des polygones simples, les assembler pour reconstituer une figure définie à l'avance devient un problème de combinatoire.
Il faut faire preuve d'ingéniosité mathématique.
Des questions complexes peuvent apparaître.
Les polyminos sont des exemples très populaires de ces puzzles raffinés pour mathématiciens amateurs et enthousiastes.
Nous allons ici jouer avec des assemblages de triangles équilatéraux.Le jeu
En 1953, Solomon W. Golomb,
alors étudiant à l'université de Harvard désigna par polyomino toute figure plane obtenue en réunissant des carrés unitaires par leurs côtés.
Golomb signala dès 1954 dans Damiers et Polyominos qu'un jeu semblable aux polyominos pouvait être basé sur les assemblages de triangles équilatéraux unitaires.
Le mathématicien de Glasgow T.H. O' Beirne a proposé dans un numéro de New Scientist de 1961 d'appeler de telles formes des polyiamonds.
Ce terme est traduit dans "jeux mathématiques du Scientific American" de Martin Gardner par polyamants.
Une figure formée de deux triangles s'appellera diamant. Avec trois ce sera un triamant, puis un un tétramant...
et pour six nous aurons un hexamant.
Les hexamants sont au nombre de douze (exactement comme pour les pentaminos).
Nous les retrouvons ci-dessous sous les noms de pistolet, parallélogramme, hexagone, serpent, canne de golf, couronne,
sphinx, chaussure, boomerang, yacht, homard et enfin papillon.
hexagone
homard
papillon
chaussure
parallélograme
sphinx
pistolet
canne de golf
boomerang
couronne
serpent
yacht
Toute figure formée par plusieurs hexamants, contient un nombre de triangles qui est évidemment un multiple de 6.
On peut reconstituer certaines figures à partir d'un recouvrement réalisé avec des hexamants.
Je propose ci-dessous de recouvrir quelques figures symétriques ou non avec les douze hexamants.
Ce n'est pas toujours facile...
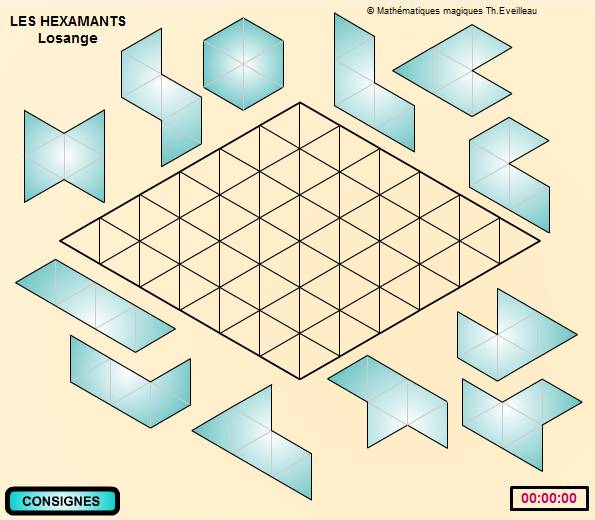
Pour jouer
Il faut recouvrir le modèle proposé avec les douze hexamants.
Dans le menu en haut de cette page, je propose diverses formes à remplir.
Glisser déplacer chaque pièce avec la souris.
En appuyant sur la flèche gauche ou droite du clavier, on retourne la dernière pièce cliquée.
En appuyant sur toute autre touche du clavier, on fait tourner cette pièce de 60° c'est-à-dire d'un sixième de tour.
Attention, ces petits jeux sont assez difficiles,
c'est pourquoi je propose en bas de la page, une solution pour chacun d'entre eux.
Le simple fait de reconstituer cette solution est un bon exercice d'observation.
C'est aussi un bon entraînement sur les transformations mises en jeu.