| Jeu
de billes sur une rangée
variante du jeu des
quilles de Kayles illustré par H.E.
Dudeney en 1878
Le
jeu
(avec
Diophante.fr)
On répartit des billes sur une même rangée de façon
aléatoire.
Par
exemple :
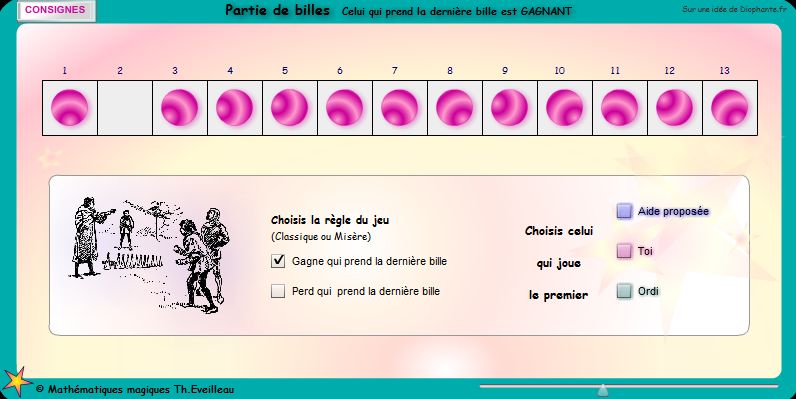
une seule bille dans la première case, une case vide et onze
autres billes qui sont accolées les unes aux autres dans les
cases restantes.
Deux
joueurs jouent à tour de rôle. Chacun peut enlever une
bille ou bien deux billes adjacentes (sans case qui les sépare).
Dans le jeu Classique, le GAGNANT est celui qui supprime
la dernière bille ou bien les deux dernières
billes adjacentes.
Dans la version dite "Misère" , le PERDANT
est celui qui enlève la dernière bille.
Existe-t-il
une stratégie gagnante ? Si oui le premier joueur est-il gagnant
?
Dans
l'animation suivante
-la première partie impose la disposition suivante : 1
bille, une case vide puis 11billes ;
-la deuxième partie donne la disposition : 1
bille, une case vide, 2 billes, une case vide, 3
billes, une case vide et enfin 4 billes.
Les configurations suivantes seront aléatoires.
Pour
jouer :
-
Choisir la version Classique ou Misère
du jeu en cochant la case adéquate.
- Choisir celui qui commence. Un clic sur Toi ou
Ordi lance le jeu immédiatement.
- Pour enlever une bille, il suffit de la cliquer.
Pour en supprimer une deuxième, attendre que la
première ait disparu.
- Cliquer le bouton Jeu Ordi pour activer
le jeu de l'ordinateur.
Si éventuellement vous avez demandé l'AIDE
proposée au début, celle-ci sera visible en glissant la
souris sur le bouton AIDE.
ATTENTION l'ordinateur utilise une stratégie efficace et s'il
joue en premier, le bouton AIDE sera sans secours efficace.
Observer le jeu de l'ordinateur et découvrir sa procédure.
Le curseur en bas à droite de l'animation permet de modifier
la vitesse de disparition des billes.
CLIQUER
Analyse du jeu
: comment gagner
Ce
jeu rappelle le jeu de Marienbad
simple ou généralisé
(si l'on considère chaque paquet de billes adjacentes,
comme une rangée d'allumettes).
Cependant la différence essentielle réside dans le fait
qu'on ne peut prendre ici qu'une bille ou deux billes adjacentes.
C'est
donc un peu plus compliqué.
La stratégie utilisée consiste à repérer
le nombre de billes adjacentes de chaque paquet.
Chacun de ces nombres est transformé avec la table suivante
(les Grundy Nimbers) :
| 0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
0 |
1 |
2 |
3 |
1 |
4 |
3 |
2 |
1 |
4 |
2 |
6 |
4 |
1 |
Une fois obtenus les correspondances des nombres avec la deuxième
ligne, les écrire en base deux.
Ex : 9
--> 4 --> 100
Les nombres binaires sont éventuellement complétés
avec des zéros à gauche de façon à ce
qu'ils aient tous la même longueur.
Nous additionnons ces nombres binaires avec la NIM-addition, ainsi
définie :
0+0 =0 ; 1+1 = 0; 1+0=1 ; 0+1=1.
Il faut trouver une situation qui annulera ce résultat avec
les nouveaux paquets.
En
effet une situation avec Nim-addition nulle donne toujours une situation
avec Nim-addtion non nulle GAGNANTE.
La différence entre la version Classique
et la version Misère intervient seulement
lors des derniers coups :
on prend ou on ne prend pas la (ou les) denrière(s) bille(s).
Il suffit à la fin de choisir entre entre 1 ou 2 billes : en
effet dans une situation gagnante on a le choix.
Les situations
proposées au départ
1°)
Exemple avec la première partie : 1 bille, un vide,
11 billes.
un
paquet de 1 --> 1 qui s'écrit 1
en binaire.
un paquet de 11 --> 6 qui s'écrit
110 en binaire.
La Nim-addition de 1 et 100 donne
001+110=111.
Situation non nulle gagnante.
On peut donc proposer la situation : supprimer la bille colonne 6)
qui laissera 1 bille, un vide, 3 billes,
un vide puis 7 billes.
un paquet de 1 --> 1 qui s'écrit 1
en binaire.
un paquet de 3 --> 3 qui s'écrit 11
en binaire.
un paquet de 7 --> 2 qui s'écrit 10
en binaire.
La Nim-addition donne 01+11+10 = 00
On a transformé la situation proposée en situation nulle
PERDANTE pour l'adversaire.
Le premier coup est ici GAGNANT.
2°)
Exemple avec la deuxième partie : 1 bille, un vide,
2 billes, un vide, 3 billes, un vide,
4 billes.
un
paquet de 1 --> 1 qui s'écrit 1
en binaire.
un paquet de 2 --> 2 qui s'écrit
10 en binaire.
un paquet de 3 --> 3 qui s'écrit
11 en binaire.
un paquet de 4 --> 1 qui s'écrit
1 en binaire.
La Nim-addition de 1 et 100 donne
01+10+11+1=01.
Situation non nulle gagnante.
On peut donc proposer la situation : supprimer deux billes à
partir de la colonne 11,
qui laissera des paquets de 1 bille, 2
billes, 3 billes, 1 bille
et 1 bille.
un paquet de 1 --> 1 qui s'écrit 1
en binaire.
un paquet de 2 --> 2 qui s'écrit 10
en binaire.
un paquet de 3 --> 3 qui s'écrit 11
en binaire.
un paquet de 1 --> 1 qui s'écrit 1
en binaire.
un paquet de 1 --> 1 qui s'écrit 1
en binaire.
La Nim-addition donne 01+10+11+01+01 = 00.
On a transformé la situation proposée en situation
nulle PERDANTE pour l'adversaire.
Ce n'est d'ailleurs pas la seule solution (voir
l'AIDE).
Le premier coup est là aussi
GAGNANT.
|
