Les 17 types de pavage (1)
Voici les noms des 17 types utilisés en cristallographie,
CLIQUER chaque nom dans le tableau pour animer le type correspondant.
Un exemple : le type p6m
Les 17 types : un algorithme de reconnaissance
Il existe cinq façons de paver le plan sans retourner les carreaux :
-translation du motif ou
-rotation du motif de 60°, 90°, 120° et 180° (symétrie centrale).
Si l'on retourne les carreaux, on trouve douze façons supplémentaires de paver le plan.
Cela donne dix-sept pavages dits "périodiques" du plan.
Les cristallographes ont déterminé et classifié au XIXème siècle tous les groupes distincts d'isométries du plan et de l'espace
(parfois sous la forme de détermination des réseaux cristallins, sans expliciter l'aspect groupal).
Le premier d'entre eux est le Français Auguste Bravais (1811-1863) qui a publié les résultats, en 1847,
sous forme d'une classification des réseaux : les 230 réseaux de Beauvais à 3 dimensions.
Par la suite, vers 1890, le cristallographe et mathématicien russe Fedorov et le mathématicien allemand
Schönflies ont indépendamment retrouvé les résultats de Bravais en les présentant dans un cadre groupal.
Evgraf Stepanovitch Fedorov a montré en 1891 (Université de Saint-Petersbourg),
qu'il n'existe que 17 types de pavage du plan (heptadécacité).
Ces types sont classés suivant l'agencement des rotations et des symétries qu'on peut y trouver.
Ils constituent ce que l'on appelle les groupes cristallographiques par analogie avec les groupes conservant les cristaux dans l'espace euclidien à 3 dimensions.
Nous regardons ici, les pavages du plan "périodiques" ou répétitifs,
c'est à dire invariants par un groupe discret de translations et, par conséquent, par un des 17 groupes cristallographiques.
Il existe toujours une isométrie qui amène un pavé sur un autre pavé quelconque, mais qui de plus conserve l'ensemble du pavage.
Ce pavage s'étend à l'infini ; il existe des translations dans des directions différentes. On peut caractériser, en partie, le pavage en décrivant son groupe.
Ce groupe contiendra toujours des translations dans plusieurs directions, mais aussi des rotations, des symétries axiales, des symétries glissées.
Les arabes ont développé de très beaux pavages géométriques.
En effet, ils ne devaient pas représenter Allah et ont puisé leur inspiration dans la géométrie.
Ils ont créé en Andalousie de merveilleux chefs d'œuvre pour décorer palais et mosquées en utilisant toutes les dispositions possibles.
Ce sont de vrais précurseurs dans le domaine des pavages.
Pour reconnaître la famille d'un pavage on peut suivre l'algorithme suivant
Voir
. l'algorithme donné par Pierre Jullien qui découvrit la méthode des enveloppes, il fut le premier directeur de l'IREM à Grenoble (1971-1976).
. les pages de Xavier Hubaut sur les groupes de pavage .
Il est arrivé avec son équipe à associer pour 15 des 17 groupes un seul type de "pavé" et pour les deux groupes restants deux types, soit au total 19 types de "pavés".
.les 19 types et l'algorithme de Dominique Ribault : http://www.polytess.info
Les noms proposés ici correspondent aux noms utilisés en cristallographie.
Le pavage est-il identique à son reflet dans le miroir ?
NON Angle minimal de rotation ?
0 Parallélogramme asymétrique
p1 180° Parallélogramme symétrique
p2 120° Hexagonal 3-rotatif
p3 90° Carré 4-rotatif
p4 60° Hexagonal 6-rotatif
p6
Nombre de directions
d'axe de symétrie ?OUI
Y-a-t-il des rotations entre les mailles ?
Si oui de quel angle ?0 0
Rectangulaire glissant
180°
Rectangulaire biglissant
1 0
Glissage ? non
Rectangulaire monosymétrique
0
Glissage ? oui
Rhombique monosymétrique
180°
Rectangulaire glissant
symétrique2 0
Rectangulaire bisymétrique
180°
Rhombique bisymétrique
90°
Carré 4-rotatif glissant
3 0
Hexagonal tri-symétrique
60°
Hexagonal 3-rotatif symétrique
4 Carré totalement symétrique
6 Hexagonal totalement symétrique
Analyse rapide de mosaïques
L'art de paver le plan (le sol, les murs, le plafond...) avec un motif relève à la fois de l'artisanat et des mathématiques.
On pave avec des carreaux.
Avec une infinité de carreaux tous identiques et avec des règles d'assemblage
adaptées, on peut remplir tout le plan, sans trou ni recouvrement.
Pour réaliser les mosaïques les carreleurs utilisent des transformations géométriques simples :
translations, rotations, réflexions et réflexions suivies de translations.
Les Musulmans décorent les édifices avec des motifs géométriques.
Ils les ont perfectionnés et élevés à un niveau de complexité et de développement jamais connus auparavant.
Dans les motifs décoratifs qui ornent les faïences au sein de l'Alhambra, se cachent
des régularités basées sur des figures répétitives, des couleurs qui suivent un modèle
de dessin et des transformations géométriques comme les symétries, les rotations et les translations.
Il y aurait exactement 17 pavages différents représentés sur les plafonds du palais de Grenade.
Une des configurations les plus rencontrées est la "pajarita" (cocotte en papier) ;
on la trouve par exemple sur la partie basse des murs du patio de los Arrayanes.
L'espace se structure en triangles équilatéraux.
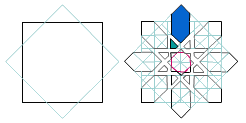
On rencontre également très souvent l'étoile à 8 ou 16 branches obtenue par rotations de carrés.
La trame des petits carrés obtenue sert de guide pour tracer les figures qui composent l'étoile et les entrelacements du dessin.
La composition finale est une sorte de labyrinthe sans fin composé de multiples formes colorées.
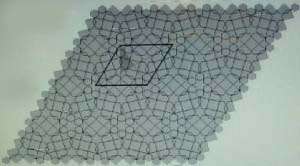
Sur les mosaïques de l'Alhambra on trouve des exemples des 17 types vus précédemment.
L'Alhambra ! L'Alhambra ! Palais que les génies
Ont doré comme un rêve et rempli d'harmonies,
Forteresse aux créneaux festonnés et croulants
Où l'on entend la nuit de magiques syllabes
Quand la lune, à travers les mille arceaux arabes,
Sème les murs de trèfle blanc.
Victor Hugo
Le palais de l'Alhambra se dresse sur une colline à l'Est de Grenade.
Chef-d'œuvre de l'art arabe il fut commencé au XIIème siècle puis
agrandi et embelli pendant près de quatre cents ans.
Télécharger un logiciel pour créer des pavages selon les types précédents ICI


(1) Voir aussi RAOUL RABA Les secrets des pavages editions Sciences & Images
A.DELEDICQ R.RABA Le MONDE DES PAVAGES ACL - éditions du Kangourou