La jeune fille et les aimants                

La jeune fille au long ruban dans les cheveux se retrouve seule dans une pièce vide, avec deux barres d'acier identiques, à ceci près que l'une est aimantée et l'autre pas. Pour être définitivement libre, elle doit déterminer celle qui est aimantée. Les barres sont lourdes, solides, INCASSABLES et aucun matériel n'est à sa disposition.

  Comment s'y prendra-t-elle ?

 

Solution   

 

 

 

 

Solution

Dans ce problème nous ne sommes capables d'aucune référence immédiate. La résolution est de type 'tout ou rien'. Mais elle peut jaillir après un travail intérieur insconscient.
La solution existe et elle est simple. Il faut rompre une symétrie. Mais ici la solution doit être purement physique et les seuls objets manipulables sont les deux barres, et ... le ruban. L'attraction magnétique est complètement symétrique par rapport aux deux barres, elle ne permet pas de dire qui attire et qui est attiré... sauf justement en un point : celui qui correspond au milieu de la barre aimantée, qui lui par symétrie ne peut être aimanté.
On détermine donc le milieu de l'une des barres B. Pour cela on 'prend' sa longueur avec le ruban. On plie en deux la partie du ruban qui correspond à la longueur de la barre pour en déterminer le milieu.
Alors, on présente l'autre A perpendiculairement au milieu de la barre B.

Si rien ne se passe, alors la barre A n'est pas aimantée, puisqu'elle n'attire pas le milieu de B. C'est donc la barre B qui est aimantée.

S'il y a attraction , c'est la barre A qui est aimantée et attire la barre B non aimantée.
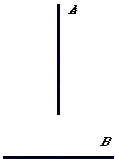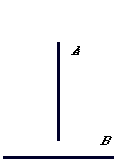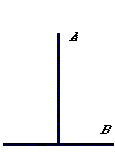