Alors que je me promenais en Grèce à Delphes emmitouflée dans mon imperméable ( il pleuvait des cordes oui... oui... ), j'entendis une voix m'interpeller près de moi. Pourtant ma famille trottinait devant... Curieuse, je me retournai tout en pensant qu'une autre personne portait le même prénom. Je découvris alors l'une de mes collègues caennaises qui marchait rapidement pour se protéger de la pluie battante. Nous nous esclaffâmes ! C'était si improbable de se rencontrer ici !
Mais était-ce donc si étonnant ?
Nous allons voir quelques cas où les mathématiques vont nous aider à prédire de tels évènements.

L'anniversaire

Annie affectueusement surnommée la Pythie par ses 50 copains et copines de voyage s'installa au beau milieu de la scène du théâtre de Delphes. Elle jeta un regard circulaire sur tous ses amis assis autour d'elle et dit :
"Je sais que deux d'entre vous vont fêter leur anniversaire le même jour".
A-t-elle raison et pourquoi ?

SOLUTION

Annie n'a pas trop de mal à jouer la prêtresse de l'oracle de Delphes !
En réalité elle a environ 97 % de chances d'avoir raison. C'est mathématique ! Mieux, comme les naissances sont pas équiréparties sur l'année, il est probable qu'Annie la Pythie ait encore plus de chance de succès.
Voici (pour simplifier prenons une année de 365 jours) :
nous allons calculer la probabilité que l'évènement prédit ne se produise pas. C'est-à-dire la probabilité qu'aucun des étudiants ait le même anniversaire : nous obtenons 365 jours possibles pour le premier, 364 pour le deuxième et ainsi de suite nous obtenons 316 jours pour le 50 ième. Ce qui nous donne 365x364x363x... 316 cas favorables.
Il y a bien sûr 365⁵⁰ cas possibles. (Car 365 possibilités pour chacun d'entre eux)
La probabilité que les anniversaires soient tous différents est donc le quotient du nombre de cas favorables sur le nombre de cas possibles :
( 365x364x363x... 316 ) / (365⁵⁰)
Ici cela donne environ : 0.0296
Donc pour avoir au moins un anniversaire commun, on trouve environ 1 - 0.0296 ~ 0.97
soit environ 97% de chance.

Résultats


Dans l'animation Flash ci-dessous entrez le nombre de personnes afin d'obtenir la probabilité d'avoir un anniversaire commun (entre ces différentes personnes).
Le plus petit nombre qui donne un résultat supérieur à 50% est 23.
Pour un nouvel essai, cliquer sur RAZ : Remise A Zéro. 

 

CLIQUER

 

 

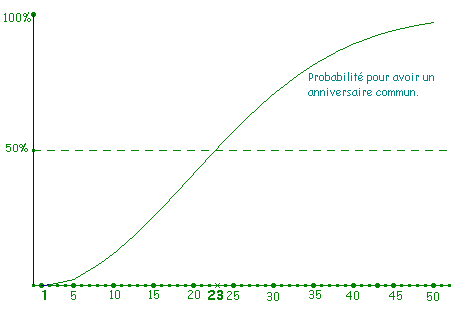
Voici la courbe donnant les chances d'avoir une coïncidence d'anniversaire en fonction du nombre de personnes.

 

Etonnant ?
     La plupart des gens sont impressionnés et trouvent cette coïncidence incroyable : en effet nous nous attendons à ce qu'il faille au moins 366 personnes pour qu'il y ait à coup sûr une coïncidence d'anniversaires puisqu'on ne dispose que de 365 jours différents (Principe des tiroirs).
ce n'est donc pas le cas. Comment pouvons-nous nous tromper à ce point ? C'est ce que nous allons essayer de comprendre avec la question suivante.

Question 2

Quelle probabilité de succès aurait Annie en prédisant qu'un de ses amis a le même anniversaire qu'elle ?

Solution

Le problème n'est plus le même car la date commune est cette fois fixée : c'est la date d'anniversaire d'Annie.
Le nombre de cas possibles est encore 365⁵⁰ car chacun a 365 possibilités d'anniversaire.
Cherchons le nombre de cas défavorables à la prédiction d'Annie. Chacun peut avoir pour date anniversaire les 364 jours de l'année autres que celui d'Annie. Cela nous donne donc pour les 50 personnes, 364⁵⁰ cas possibles.
La probabilité que les anniversaires soient tous différents de celui d'Annie est toujours le quotient du nombre de cas défavorables sur le nombre de cas possibles. Ici cela donne
( 364⁵⁰ ) / (365⁵⁰ ) = (364/365) ⁵⁰
soit environ 0.87
La probabilité que l'un des 50 amis ait le même anniversaire qu'Annie est environ 1 - 0.871 soit à peu près 12.9%.
Donc Annie n'aurait qu'à peine 13 chances sur 100 d'avoir raison... un peu moins d'une chance sur 8.

Remarque La formule de Stirling nous donne une très bonne approxiamation de factorielle n pour les grands nombres :
Dans cette formule e ~ 2,71828 est le nombre exponentiel appelé aussi constante de Néper.

Résultats

Dans l'animation Flash ci-dessous entrez le nombre de personnes (autres que Annie) afin d'obtenir la probabilité d'avoir le même anniversaire qu'Annie.
Nous constatons que le plus petit nombre qui donne un résultat supérieur à 50% est 253.
Pour un nouvel essai, cliquer sur RAZ : Remise A Zéro. 

 

 

 

Question 3

Considérons maintenant que les 50 personnes ont des anniversaires différents.
Quelle probabilité de succès aurait Annie en prédisant qu'un de ses amis a le même anniversaire qu'elle ?

SOLUTION

Le nombre de cas possibles pour avoir des anniversaires tous différents (sans tenir compte d'Annie)
est de 365 x 364 x 363 x ... x (365-50+1) car le premier a 365 anniversaires possibles, le deuxième 364 etc.
On a donc 365x364x363x ... x316 cas possibles.

Cherchons le nombre de cas favorables à la prédiction d'Annie.
Tous les anniversaires sont différents entre eux et différents de celui d'Annie. Ce qui donne 364 cas pour le premier, 363 pour le deuxième puis 362 pour le troisième et ainsi de suite. Le cinquantième aura (364-49) soit 315 possibilités. 
Tout cela fournit 364x363x362x361x...x315 cas.

La probabilité que les anniversaires soient tous différents de celui d'Annie est le quotient du nombre de cas défavorables sur le nombre de cas possibles. Ici cela donne :
(364x363x362x361x...x315 ) / (365 x364x363x362x...x316) = 315 / 365
soit environ 0.863
Et la probabilité que l'un des 50 amis ait le même anniversaire qu'Annie est environ 1 - 0.863 soit à peu près 0.137 donc un peu moins de 14%.
Ce dernier résultat est un peu meilleur que le précédent ce qui est logique.

Pour n personnes nous aurions 1 - [ (365-n) / 365 ]

Résultats

Dans l'animation Flash ci-dessous entrez le nombre de personnes (autres que Annie, toutes ayant des anniversaires différents) afin d'obtenir la probabilité d'avoir le même anniversaire qu'Annie.
Nous constatons que le plus petit nombre qui donne cette fois un résultat supérieur à 50% est 183.
Pour un nouvel essai, cliquer sur RAZ : Remise A Zéro. 

 

 

 

Finalement

Nous confondons inconsciemment les 3 questions précédentes et notre intuition nous joue des tours nous faisant croire à des évènements exceptionnels.
Dans [REJW] (2) nous découvrons que si l'on demande à 10 personnes d'inscrire un nombre entre 1 et 100 sur une feuille de papier, il y a plus d'une chance sur trois (à peu près 37% de chances ) pour que deux personnes choisissent le même nombre.
Exactement : 1 - [(100x99x98x... x91)/(100 ¹⁰)]
Si l'on prend 20 personnes alors on augmente les chances qui passent à plus de 87%. De quoi lancer un numéro de télépathie ...
G.Charpak et H.Broch dans Devenez sorciers Devenez savants nous montrent comment à la télévision un 'médium' fait griller des ampoules à distance. En réalité, le calcul prouve que statistiquement pendant l'émission au moins 2 000 lampes des millions de téléspectateurs vont griller très naturellement parce qu'elles sont usagées. Ce sont ces personnes qui en feront part et... satureront le standard téléphonique assurant le succès du 'médium' !

 

 

Les horoscopes

Bertram Forer publia le premier article sur ce sujet en 1949. La plupart des affirmations des horoscopes par exemple sont "vraies" pour la majorité des gens. Celles qui ne le sont pas sont pratiquement ignorées au profit de celles détenant une part de vérité.
Ainsi des chercheurs ont démontré que si on cache les signes d'un horoscope, les gens sont incapables de reconnaître le texte qui les concerne, mais que lorsque les signes sont apparents, ils sont convaincus que ce qui est écrit sous leur signe leur correspond le mieux.

CONCLUSION...

Quel rapport avec ma rencontre surprise à Delphes avec ma collègue caennaise ? Tout simple : la plupart des enseignants dont je fais partie ont une prédilection pour la Grèce. Delphes est un passage presque obligé. De surcroît pendant les vacances de Pâques la Grèce connaît généralement un climat agréable ( hum... ;-). Les chances d'y croiser un ou une collègue ne sont pas si petites.
Nous aimons parler de coïncidence quand il y a souvent des explications très simples et rationnelles.

Rob Eastaway parle de l'effet Barnum, qui est la tendance des gens à donner plus de signification à une situation qu'elle n'en a réellement. Nous avons souvent une mémoire sélective et nous nous souvenons plus particulièrement des évènements non courants et "exceptionnels". De nombreux phénomènes de voyance, d'astrologie sont basés sur ces résultats.

Bien sûr il des coïncidences exceptionnelles, on peut gagner le gros lot au loto ;o)

Petite histoire : le professeur étourdi (source : le livre qui rend fou de Raymond Smullyan )
Un professeur expliquait un jour à ses 19 étudiants qu'il y avait moins de 50% de chances que deux d'entre eux aient le même anniversaire. Pourtant l'un de ses étudiants affirma : "Malgré tout ce que vous dites je vous parie qu'il y a au moins deux personnes dans la classe qui ont leurs anniversaires le même jour ! ".
Le professeur objecta : "Les probabilités étant largement en ma faveur il n'est pas honnête que j'accepte un tel pari". "ça ne fait rien" répliqua l'étudiant".
Persuadé de lui donner une bonne leçon, le professeur fit l'appel pour demander les dates de naissance, mais, arrivé vers la moitié de la classe, il s'arrêta et tous éclatèrent de rire devant son étourderie. Pourquoi ?

Réponse : parce qu'il avit oublié qu'il y avait des jumeaux dans sa classe.

 

 

(1) Voir IAN STEWART L'univers des nombres éditions BELIN Pour la science
(2) ROB EASTEWAY JEREMY WYNDHAM Pourquoi les bus arrivent-ils toujours par trois ? éditions Flammarion