Le
problème
On
choisit au hasard une corde dans un cercle donné.
Quelle est la probabilité pour que la longueur de cette
corde soit supérieure au côté du triangle équilatéral
inscrit dans le cercle ?
Anatole, Barnabé et Camille proposent ci-desous trois solutions
très simples, a priori inattaquables et confortées par
l'expérimentation.
Pour chaque solution, une première animation simule le tirage
des cordes et se termine par un petit commentaire. Une deuxième
animation permet de visualiser l'évolution d'une corde dans
un cas particulier.
Les trois approches aboutissent à des résultats différents...
On pourrait d'ailleurs imaginer d'autres approches...
C'est très troublant. Quelle conclusion en tirer ?
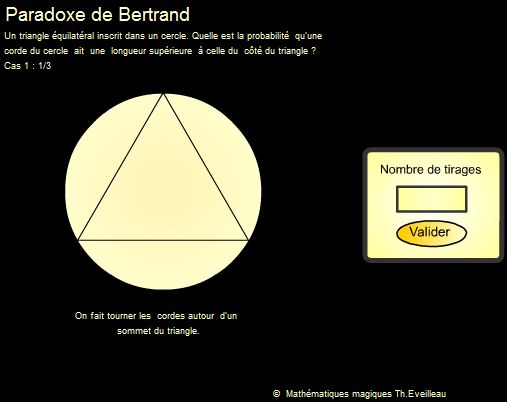
Solution d'Anatole
Tous
les points du cercle ont la même probabilité de constituer
une extémité de corde.
Dans la simulation les cordes sont choisies au hasard. Plus il y a
de cordes et plus la probabilité se rapproche de 1/3.
CLIQUER
Petite explication
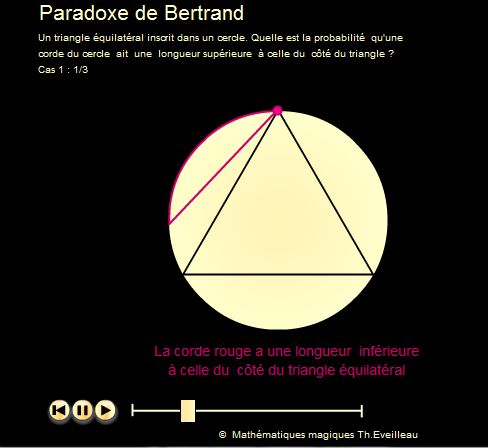
Cette animation fait tourner une corde autour d'un sommet du triangle
équilatéral inscrit.
Les cordes qui conviennent sont à l'intérieur du
triangle équilatéral.
L'arc vert correspond à 120° et l'arc rouge à
240°. La
probabilité cherchée est donc de 1/3.
CLIQUER
L'arc
vert correspond au tiers du cercle entier.
Solution
de Camille
On choisit un
point quelconque comme milieu de la corde à tracer. Dans la
simulation ci-dessous, on choisit au hasard un milieu I dans le disque.
La corde est alors déterminée de façon unique,
sa direction est la perpendiculaire au segment joignant le centre
du cercle et le point I.
CLIQUER

Petite explication
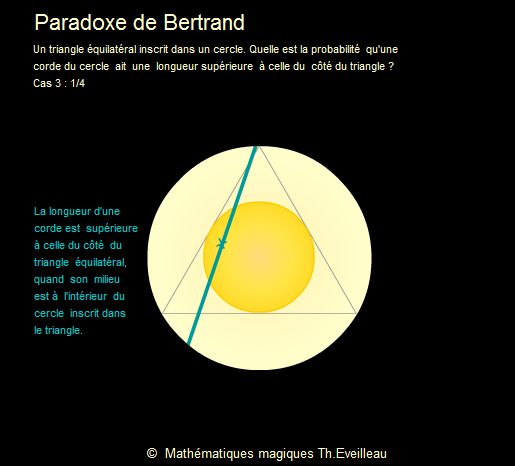
La corde est plus longue que le côté du triangle si
et seulement si son milieu est à l'intérieur du cercle
inscrit. Or le rayon du cercle inscrit au triangle équilatéral
est égal à la moitié du rayon du cercle circonscrit.
L'aire du cercle inscrit est donc égale au quart de l'aire
du cercle circonscrit (c'est à dire (1/2)2
).
Le rapport des aires, 1/4 est cette fois la probabilité
cherchée.
CLIQUER
On pourrait faire un quatrième calcul
Le côté du triangle équilatéral inscrit
dans un cercle de rayon R est R et le diamètre est 2R ;
et le diamètre est 2R ;
Les cordes acceptables ont une longueur comprise entre R et 2R. Les longueurs possible vont de 0 à 2R.
et 2R. Les longueurs possible vont de 0 à 2R.
La probabilité cherchée est donc (2R - R ) / 2R
) / 2R
soit 1 - 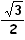
Ce quatrième
résultat ne simplifie pas les choses...
EXPLICATION
Il
semble clair que les quatre hypothèses de répartition
sont également réalisables.
Cependant il n'y a pas vraiment
de paradoxe, on a des conditions expérimentales différentes.
Il s'agit d'un choix de conditions qui conduisent à des évènements
différents.
Le problème est simplement mal posé : la phrase "choisir
au hasard une corde dans un cercle" n'a pas une interprétation
unique.
C'est toute une
histoire...
L'expression 'au hasard' devrait signifier
que les cordes sont 'équiprobables', mais nous n'avons aucune
mesure sur l'ensemble continu de toutes les cordes. On manipule ici
implicitement plusieurs espaces probabilisables avec un énoncé
trop imprécis.
Un paradoxe qui n'en est pas un
En fait ce "paradoxe" illustre simplement la nécessité,
exprimée par Kolmogorov dans son axiomatique des probabilités,
de définir l'espace probabilisable avant de définir
la probabilité.
Ce paradoxe n'a donc rien de mystérieux. Si l'on trouve des
probabilités différentes c'est tout simplement parce
qu'on se situe, au moment des choix aléatoires, dans des espaces
(des univers) différents.
Les conditions expérimentales
de tirage des cordes ne sont pas identiques dans les différents
cas
.
Choisir une corde par une extrémité, le milieu, une
direction ou une longueur n'est pas équivalent.
- La première solution suppose que l'angle,
de la corde avec la tangente au cercle menée par le sommet
fixe, a une distribution de probabilité uniforme sur [0, 180°].
- La deuxième solution suppose que la probabilité
de la variable milieu de la corde a une distribution uniforme sur
le diamètre du cercle initial.
- La troisième solution suppose que la variable
milieu de la corde a une distribution uniforme sur la surface intérieure
au disque initial.
Quand on aborde une situation où l'infini intervient tout se
complique !
Comme le dit Lebesgue :"lorsque nous faisons intervenir l'infini,
nous n'obtenons pas les mêmes théorèmes..."
La notion de pur hasard ou d'équiprobabilité devient
'délicate'.
Choisir au hasard entre un nombre infini de cas n'est pas une condition
suffisante. Il faut définir au préalable comment on
va mesurer l'ensemble en question. Le problème réside dans le fait
qu' il est difficile de mesurer des ensembles infinis.
On sait par exemple qu'il y a autant de pairs que de nombres entiers
(leurs moitiés...), qu'il y a autant de réels positifs que
de réels compris entre 0 et 1...
Ce
paradoxe de Joseph Bertrand célèbre par la simplicité
des différents résultats a donné lieu à
de nombreuses controverses. Il a montré la limite des définitions
des probabilités ( incorrectement définies dans le continu
) et a été historiquement un moteur dans la construction
de la théorie des probabilités actuelles.
.Kolmogorov (Théorie générale de la mesure
et théorie des probabilités 1929) a axiomatisé
le calcul des probabilités.
.Henri Poincaré a fait une étude de ce paradoxe dans
le "Calcul des probabilités" .
.Emile Borel s'est intéressé également au calcul
des probabilités et a introduit une approche basée sur
la théorie de la mesure. Il définit un ensemble de mesure
nulle et ce qu'on appelle maintenant un ensemble borélien.
.Henri Lebesgue reprendra le travail de Kolmogorov.
Petite
devinette
.une fille : "j'ai autant de frères que de sœurs"
.un de ses frères : "moi, j'ai deux fois plus de sœurs
que de frères".
Combien sont-ils ?
Une
petite mise en équation donne 4 filles et 3 garçons
donc ils sont 7.