 Le
cercle à double centre
Le
cercle à double centre
Construisons
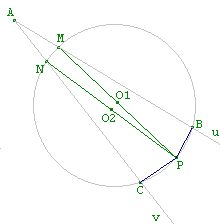
un angle (Au,Av) quelconque.
Prenons deux points quelconques B et C sur chacun des côtés
de cet angle.
Traçons la perpendiculaire au côté [Au)
en B, puis traçons la perpendiculaire au côté
[Av) en C.
Ces deux perpendiculaires se coupent en un point P.
Le cercle (C)
passant par les trois points C, P et B coupe
les deux côtés de l'angle (Au,Av) en M et N.
|
|
Le triangle
MBP est un triangle rectangle en B,
il est donc inscriptible dans un cercle de diamètre
[MP], dont le centre est le
milieu de [MP]. Soit O1 ce centre.
Or les points B, P et M sont situés sur le cercle (C)
.
O1 est donc le centre de (C).
Nous démontrons de la même façon que O2
milieu de [NP] est le
centre du cercle (C).
|
Finalement
le cercle (C)
a deux centres O1 et O2 .
Où
est l'erreur ?
 Solution
Solution
La
figure ci-dessus est fausse, en effet (BP) n'est pas parfaitement
perpendiculaire à (AB), pas plus que (CP) ne l'est à
(AC).
Lorsque
les droites (BP) et (CP) sont perpendiculaires respectivement aux
côtés (MP) et (NC), alors le point d'intersection A se
trouve confondu avec M et N :
[AP] est un diamètre du cercle
(C)
passant par les
points A , B et P et
de la même façon [AP] est un diamètre
d'un cercle (C
') passant
par les points A , C et P.
On
a forcément (C
')
confondu avec (C)
puisque ces deux cercles ont même diamètre.
Les côtés [MP] et [NP] sont confondus
avec [AP] et sont l'hypoténuse commune aux triangles
rectangles MBP et NCP.
Le quadrilatère A BPC qui a deux angles droits opposés
est bien inscriptible dans le cercle
(C).
Nous pouvons vérifier cela sur l'animation exacte ci-dessous.
On peut déplacer chacun des points B
et C sur les côtés de l'angle (AB, AC).
On peut modifier l'angle en déplaçant verticalement
les points D et E.
Ces déplacements peuvent être effectués avec la
SOURIS ou bien avec le CLAVIER :
-flèches GAUCHE et DROITE pour les points B et C ;
-flèches HAUT et BAS pour les points D et E.