La revanche de Cycleux Cela devenait insupportable, Un 1 et Cycleux 0,785785... A la traîne interminable et périodique     sept huit cinq sept huit... Se promenaient comme d'habitude sur la plage. Un se moquait encore des empreintes infinies Que laissait Cycleux dans le sable. De plus Un se vantait d'être rigoureux, Chacun connaissait sa valeur exacte. Quant à Cycleux, il n'était pas apprécié à sa juste valeur. On pouvait l'approcher d'aussi près que l'on voulait, Encore plus près et même encore... , Mais bon, on ne l'atteignait pas ! Ah, cette infinité de décimales !                                    ©Th.E     ALORS... Cycleux n'y tint plus, et contre vents et marées il réfléchit et sut : il allait retourner la situation. Il  se transforma avec un nombre fini de chiffres et Un devint cycleux. Comment donc ?      Explication              1 devint 0,9999...                   et             0,785785... devint 785 / 999 Les points de suspension signifient qu'on ne s'arrête jamais... Démonstration : On a effectivement            1 = 0,9999...                   et           0,785785... = 785 / 999   Vous pouvez déja vérifier sur votre calculette, oui enfin mais... elle n'affiche qu'un nombre fini de chiffres ... peut-être qu'avec plus de chiffres...?   Regardons donc de plus près avec ceux qui n'ont pas peur de l'infini (lycéens)   Posons x = 0,999... (infinité de 9) 10 x = 9,999... donc 10 x = 9 + 0,999... soit 10 x = 9 + x soit 10 x - x = 9 et 9 x = 9 on a alors x = 1 soit 1 = 0,999... Posons x = 0,785785... (infinité de chiffres) 1000 x = 785,785... donc 1000 x = 785 + 0,785785... soit 1000 x = 785 + x soit 1000 x - x = 785 et 999 x = 785 on a alors x = 785/999 soit 785/999 = 0,785785... Si vous doutez ou n'appéciez pas cette écriture, trouvez un nombre plus grand que 0,999.... et plus petit que 1. C'est impossible... s'ils étaient différents on en aurait une infinité. Certains résolvent la difficulté en disant que le nombre 0,999.... avec une infinité de 9, n'existe pas !   Depuis ce jour Cycleux se promène sur la plage le coeur très léger. Morale : il ne faut jamais se moquer de plus long que soi. .Démonstration utilisant une progression géométrique 0,9999... est la somme de la suite infinie des termes d'une progresson géométrique :
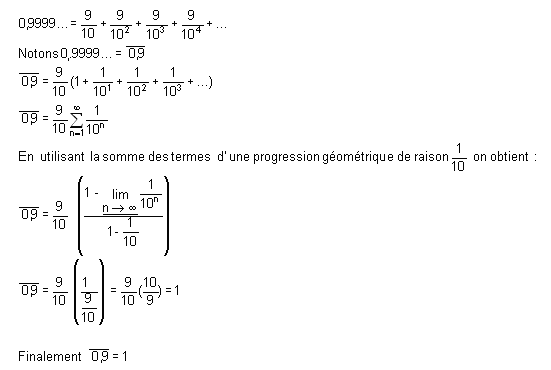