Le problème

On m'a envoyé le problème suivant qui m'a laissée perplexe un moment :
nous avons deux raisonnements différents apparemment corrects pour cet exercice de lycée. On devrait trouver les mêmes solutions.
Avant de lire mon analyse, essayez de comprendre les solutions des deux élèves. Peut-être aurez-vous une autre interprétation.

Analyse

Modeste
remplace directement dans l'équation (1) proposée les valeurs de la variable x par les valeurs désirées p et q.
D'abord la valeur p dans (1) --> p² + p.p + q = 0 ;
puis la valeur q dans (1) --> q² + p.q + q = 0.
Cela mène à une résolution d'un système à deux équations et deux inconnues.

A cause du degré 2, on trouve deux couples de solutions :
-dans le premier cas, les valeurs de p et q sont différentes et
-dans le deuxième cas les valeurs de p et q sont égales.

Vérifions les résultats en reportant les valeurs trouvées dans l'équation (1) proposée :
-premier cas
  p = 1 et q = -2 alors (1) devient   x² + x - 2 = 0
  p est solution car 1² + 1 - 2 = 0. C'est OK.
  q est solution car (-2)² - 2 - 2 = 0. C'est OK.

-deuxième cas
  p = - et q = - alors l'équation (1) devient   x² - x -
  p et q sont solutions car (-)² - (-) - = 0. C'est OK.
  Notons que la deuxième racine de cette équation est... non pas - mais 1 !
Ne commencez-vous pas à entrevoir une explication ?
  
Le raisonnement de Modeste est simple et tout à fait correct.
La procédure ne fait appel à aucune relation spécifique aux équations du second degré, d'où peut-être la modestie de la solution.

Prudence
utilise les relations donnant le produit et la somme des racines d'une équation du second degré lorsqu'elles existent.
Si S est la somme des deux racines et si P est le produit alors on sait que les racines de (1) sont solutions de l'équation :
x² - S x + P.
Ce raisonnement est correct si l'on cherche les deux racines de l'équation (1).
Cela reste correct si les racines de l'équation sont confondues et donnent une racine double de l'équation.
Alors pourquoi ne trouve-t-on pas la deuxième solution proposée par Modeste ?

 

EXPLICATION
Il s'agit essentiellement d'une difficulté de français dans la compréhension du texte.
Modeste et Prudence ne répondent pas à la même question.

Modeste cherche deux valeurs p et q qui seront solutions de l'équation.
Peu importe si p et q représentent une seule racine de l'équation.
Dans le texte, il n'y a pas d'article devant le mot 'solutions'.
Cela veut dire que l'on cherche certaines solutions de l'équation, mais pas forcément toutes les solutions ou racines.

Prudence elle, cherche deux valeurs qui seront les deux racines simples ou doubles de l'équation.
Ses deux valeurs de p et q seront en quelque sorte 'liées'.
Elle se sert donc à la fois de la somme et du produit des racines de cette équation.

La solution de Prudence répond à la question suivante :
    " Trouver les valeurs de p et q pour lesquelles p et q sont les solutions de l'équation (1).".

Toute la différence réside dans l'utilisation implicite par Prudence de l'article défini 'les'.
Ce n'est pas ce qui est demandé.

Observons bien
La solution - , trouvée par Modeste n'est pas une racine double de l'équation x² - x - .
C'est une des racines, l'autre est 1 qui ne correspond ni à p ni à q.
C'est pour cela que Prudence ne la trouve pas.

Avec - comme racine double, l'équation serait (x - )² = x² - 2 x +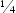
Cette équation correspond à p = -2 et q = 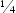et ne satisfait pas les conditions imposées.

CONCLUSION
Modeste répond au problème posé. Ce n'est pas le cas de Prudence.
Ce ne sont pas les connaissances mathématiques des deux élèves qui sont en cause, mais l'interpétation linguistique du texte.

Le français est indispensable aux mathématiques !