|
Le
triangle prétentieux
 Quelconque
il se croit régulier
Ce
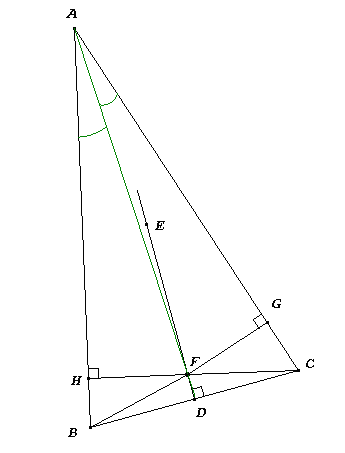
triangle ABC est quelconque.
On trace la médiatrice de [BC] passant par son milieu
D, soit E un point de cette médiatrice. Considérons
la bissectrice de l'angle A.
Si
la droite (DE) et la bissectrice sont parallèles, c'est
que cette bissectrice est perpendiculaire à [BC], elle
est alors hauteur dans le triangle ABC, qui est par conséquent
isocèle en A, puisqu'il a une bissectrice qui est aussi hauteur...
Finalement (DE) et la bissectrice sont confondues.
Si
la droite (DE) et cette bissectrice ne sont pas parallèles,
elles se rencontrent, appelons F ce point de rencontre.
| 
|
Traçons
[FB] puis [FC].
Traçons aussi [FH] perpendiculaire à (AB)
et enfin [FG] perpendiculaire à (AC) .
Les triangles AFG
et AFH sont égaux, car ils ont un côté commun
et deux angles égaux (donc les trois angles
égaux).
On en déduit : AH=AG et
FH=FG.
FB=FC (car F sur médiatrice de [BC]).
De même encore,
les triangles FGC et FHB sont égaux (un angle droit
et deux côtés égaux (hypoténuse
et un côté de l'angle droit, donc trois côtés
égaux avec le théorème de Pythagore)
: FB=FC et FH=FG).
On en déduit : HB=GC.
Avec la relation
AH=AG
ci-dessus et
HB=GC,
on trouve par addition : AB = AC.
|
Et
le triangle ABC quelconque d'affirmer : il est isocèle en A.
Mieux, on peut recommencer la démonstration avec le sommet B
ou même le sommet C, il est aussi isocèle en B et isocèle
en C. Conclusion,
il prétend beaucoup plus : il s'affirme équilatéral
!
Où
est donc l'erreur ?
Solution
Je
ne vous ferai pas languir... L'erreur est fréquente. Elle ne
réside pas dans ce qui est écrit. Mais ... elle se trouve
dans la figure ci-dessus, elle est fausse !
-Où donc ?
Nous
avons effectivement considéré deux cas :
-celui ou les deux droites (DE) et la bissectrice sont ou ne sont
pas parallèles.
Très bien, elles ne sont pas parallèles, elles
se coupent effectivement mais pas à l'intérieur du
triangle. Elles se coupent à l'extérieur.
Il faut donc se méfier
des constructions trompeuses. Ici il y a un petit défaut de
construction dans la bissectrice, qui est inexacte. Bien sûr
une figure permet de visualiser et c'est important. Mais elle doit
être rigoureuse et de toute façon, elle restera toujours
un cas particulier parmi tant d'autres.
Sur une figure rigoureuse
on constatera (voir Figure
dynamique) que les droites
concernées se coupent à l'extérieur du
triangle.
Réfutation
Le
triangle ne désarme pas. Puisque le point F est extérieur
au triangle, on recommence :
| Prenons
[FH] et [FG] perpendiculaires à (AB)
et (AC) comme ci-dessus.
Comme ci-dessus, on trouvera que les triangles AFH et AFG sont
égaux. (donc FH=FG, AH=AG);
Puis
BHF et CFG sont égaux
(car FC=FB
( F sur médiatrice de [BC]) et
FH=FG et angle droit).
De même pour les triangles AFB et AFC.
On déduit alors les égalités :
AH = AG et
HB = GC.
Le raisonnement reste identique. Mais cette fois, on soustrait
les résultats pour obtenir :
AH - HB = AG - GC
d'où à nouveau l'égalité des segments
AB et AC. |
|
Et ... notre triangle
ABC confirme qu'il est isocèle et même équilatéral
...
Solution
Cette
fois, le point F est bien à l'extérieur du triangle,
mais les points G et H sont mal placés relativement aux côtés
[AC] et [AB]. Si G est dans le prolongement de [AC]
alors H est situé entre A et B. De même si H est dans
le prolongement de [AB], alors G est entre A et C.
La démonstration
précédente est donc en défaut puisqu'on ne peut
pas soustraire les longueurs des segments dans chacun des membres
de l'équation proposée.
La figure dessinée
ici, est fausse et irréalisable. A vérifier ci-dessous,
où cette fois, c'est sûr la figure est rigoureuse...
;-)
Figure
dynamique
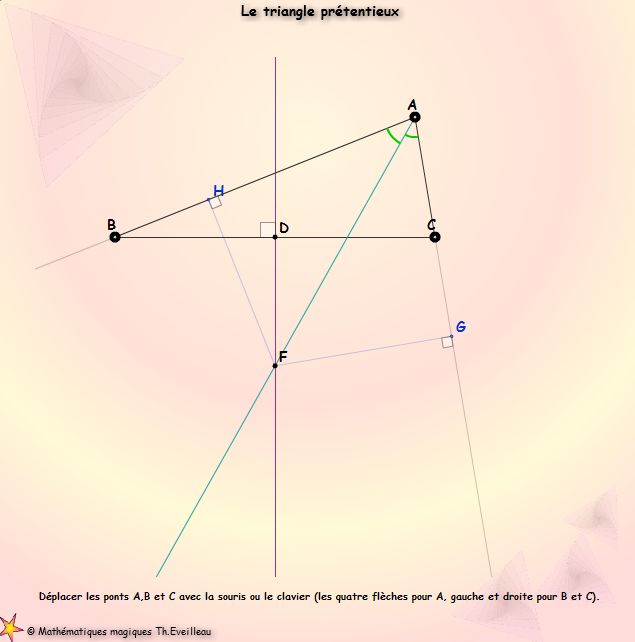
La
figure ci-dessous est cette fois parfaitement exacte
Déplacer les sommets du triangle pour s'en convaincre.
On peut les
déplacer avec la SOURIS ou bien avec le CLAVIER :
- flèches GAUCHE, DROITE pour les quatre points,
- le point A peut également être déplacé
avec les flèches HAUT et BAS.
Observer
la figure :
Si G est dans le prolongement de [AC] alors H est situé entre
A et B.
De même si H est dans le prolongement de [AB], alors G est entre
A et C.
CLIQUER
|
