A bicyclette Quand on partait de bon matin Quand on partait sur les chemins A bicyclette Nous étions quelques bons copains Y avait Fernand y avait Firmin Y avait Francis et Sébastien Et puis Paulette .L'énigme ...................................................................... .Pédalons avec l'équation de la tractrice puis laissons-nous mener... et en boucle au hasard .Exemples avec l'équation de la tractoire .Autres exemples en cabrijava ATTENTION seulement sous Internet Explorer ...................................................................... Principe des animations ...................................................................... Un traceur de courbes paramétrées ICI .L'énigme que m'a proposée Diophante Cf aussi " Which way did the bicyle go ? " Dans quelle direction, roulait le vélo qui a tracé, selon Emilie, cette sorte de bicorne de polytechnicien ? Est-ce un vélo d'adulte ou d'enfant ? Cette trace est réalisée au 1/50 ème. Comment déterminer la solution ? Pour trouver la solution, notons que les empreintes de la roue avant varient beaucoup plus que celles de la roue arrière. Vous pouvez le vérifier en observant les animations. Selon la donnée de la tractoire (roue arrière ) ou bien celle de la tractrice (roue avant) le parcours de la bicyclette est plus ou moins saccadé. La courbe qui dévie le plus (la noire dans l'exemple proposé) est forcément la trace de la roue avant. Il faut maintenant déterminer la direction du trajet Traçons des lignes tangentes à l'empreinte verte de la roue arrière en plusieur points. Chaque ligne coupe l'empreinte violine de la roue avant en deux points un à gauche et un à droite. 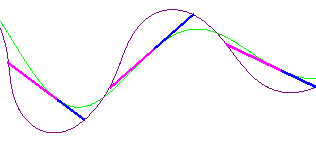Nous obtenons les segments roses à gauche et bleus à droite. Les segments roses sont tous de même longueur. Ce n'est pas le cas des bleus. Le vélo circule dainsi de droite à gauche. Chaque segment rose mesure 1,6 cm. L'échelle est au cinquantième. La bicyclette a donc un cadre de 80 cm. C'est le vélo d'Emilie qui vient d'avoir sept ans.   Voici maintenant la solution en cabrijava (sous Internet Explorer uniquement) avec la courbe d'équation y = exp(-x/7) sin(x) Laisser la souris dans le cadre pour voir le déplacement du segment représentant la barre de la bicyclette. On relance le déplacement du segment (modélisant la barre de la bicyclette) en double cliquant dans le cadre de l'animation. La roue arrière est verte et la roue avant est rose. Si l'animation s'arrête, replacer la souris dans le cadre. Voir aussi ICI en flash, prendre le deuxième exemple avec la courbe   exp(-x/7) sinx   dans le sens droite gauche. Cette situation évoque la courbe du chien qui suit son maître au bout d'une laisse tendue de longueur constante. La courbe du maître est la TRACTRICE et celle du chien la TRACTOIRE. Nous allons voir que le résultat est sensiblement différent selon que l'on s'impose l'équation de la tractrice (qui correspond à la réalité) ou bien celui de la tractoire. Pédalons .La TRACTRICE suit une équation définie à l'avance (roue avant) Je propose ici différentes fonctions pour la tractrice et choix de la direction. Faire défiler les fonctions à l'aide de la flèche. Ensuite cliquer la fonction désirée et choisir la direction. CLIQUER Fonctions paramétrées pour la TRACTRICE CLIQUER Guidons le vélo Il suffit de guider le vélo avec la souris. CLIQUER   Laissons-nous mener... Cette fois, le parcours est totalement aléatoire, la roue avant mène son train entraînant la roue arrière sur un divertissement de Mozart. Les traces des roues s'estompent avec le temps... CLIQUER   Exemples avec équation de la TRACTOIRE .La TRACTOIRE suit une équation définie à l'avance (roue arrière) Je propose ici les fonctions pour la tractoire avec le choix de la direction. Faire défiler les fonctions à l'aide de la flèche. Ensuite cliquer la fonction désirée et choisir la direction. Ce tracé est artificiel car la bicyclette est ici dirigée par le tracé de la roue arrière ce qui évidemment ne correspond pas à la réalité. Le parcours de la roue avant est donc plus saccadé et de temps en temps quand la trajectoire de la roue arrière n'est pas dérivable en un point, la roue avant fait une pirouette... Cependant il est intéressant de comparer ces parcours avec ceux correspondant aux mêmes équations pour la tractrice. Les traces de la bicyclette s'avèrent sensiblement différents pour certaines fonctions. 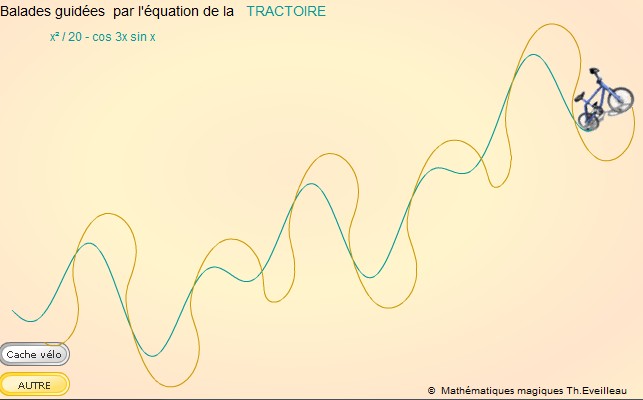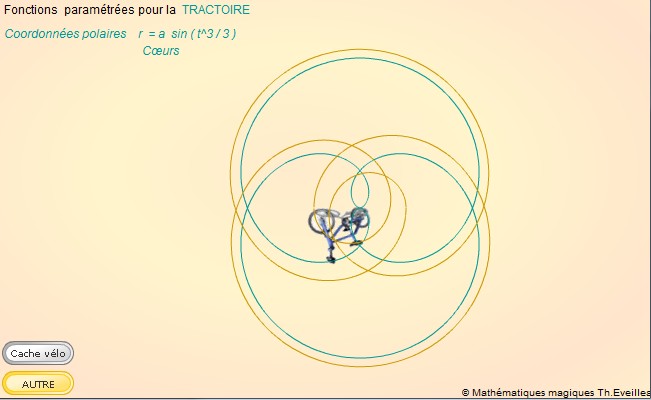CLIQUER       Fonctions paramétrées pour la TRACTOIRE CLIQUER     Exemples en Cabrijava (roue arrière) ATTENTION ces exemples animés en Cabrijava ne tournent que sous Internet Explorer .Choisir une courbe dans le tableau et cliquer sur le lien correspondant .Tractoire 3 cos x + 2 sin x .Tractoire cos² x/3    .Tractoire cos² x + cos x   .Tractoire cos x + sin x  .Tractoire courbe de Lissajous .Tractoire ICI .Tractoire cercle   .Tractoire en ellipse .Tractoire en épicycloïde .Tractoire en pétale .Observons simultanément les deux parcours gauche droite et droite gauche avec la tractoire cos x tracée en vert Si l'animation s'arrête, replacer la souris dans le cadre. .Deux traces non rectilignes qui semblent vouloir se confondre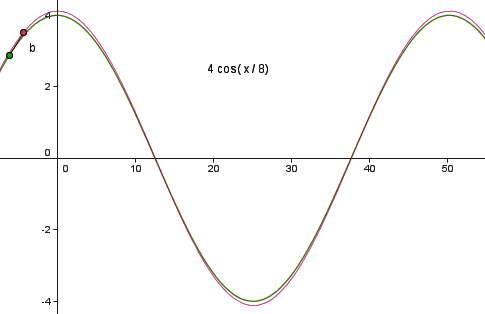 Les animations J'utilise le principe de la ' COURBE du CHIEN ' . Le maître est ici représenté par la roue avant et le chien par la roue arrière. Simulation partant de la tractrice, courbe du maître ou de la roue avant de la bicyclette Le maître avance d'une façon régulière en tenant son chien au bout d'une laisse tendue de longueur fixe. Le chien se dirige toujours vers le maître à la même vitesse. A chaque pas du maître de M0 vers M1 puis de M1 vers M2.                 - il garde une distance constante par rapport à son maître : la laisse est tendue ;         - le chien change instantanément de direction et s'oriente vers celui-ci : de C0 vers C1 puis de C1 vers C2.         C0, C1 et M1 sont alignés puis C1, C2 et M2... La réalité correspond à de très petits déplacements.   Ce sont ces deux propriétés que j'utilise dans la simulation partant de l'équation de la tractrice. La roue avant suit la tractrice et la roue arrière se repositionne instantanément : direction et distance. 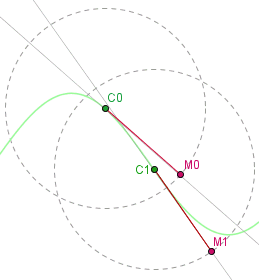Simulation partant de la tractoire, courbe du chien ou de la roue arrière de la bicyclette La trajectoire du chien est à chaque instant         - tangente à la direction de sa laisse.         - à une distance constante du maître. Partant de la tractoire, donc de la courbe du chien, il suffit de         - 'prendre' la tangente et         - reporter une distance constante dans un sens donné pour trouver la position du maître. Ce sont ces deux propriétés que j'utilise dans la simulation partant de l'équation de la tractoire. La roue arrière suit la tractoire et la roue avant est positionnée sur la tangente à la tractoire (tangente au point de contact de la roue arrière) à bonne distance et dans le bon sens. Pour en savoir plus mathématiquement , allez visiter : http://www-cabri.imag.fr/abracadabri/Courbes/Tract/Tract1.html puis les superbes tractoires acrobatiques de R.Ferréol ici : http://www.mathcurve.com/courbes2d/tractrice/tractoire.shtml Et enfin le site de David L. Finn. http://www.rose-hulman.edu/~finn/research/bicycle/tracks.html Cette deuxième adresse donne des exemples de trace unique. http://www.rose-hulman.edu/~finn/research/unicycle/unicycle.html Dans la page suivante , les traces avant et arrière sont identiques : http://www.rose-hulman.edu/~finn/research/bicycle/tracks_animate1.htm Ecouter ICI le canon de Bach sur l'anneau de Moebius (lien externe).