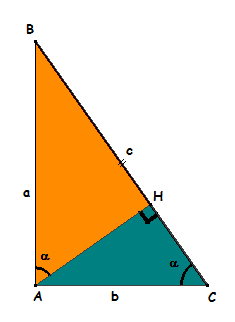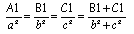La
plus belle démonstration
.Si
plusieurs triangles rectangles, ont un angle (différent de
l'angle droit) de même mesure alors ils sont semblables : chacun
a même forme que les autres. Chacun est donc un agrandissement
ou une réduction d'un autre.
Si deux triangles rectangles ont
un angle α
(autre que l'angle droit)
de même mesure et s'ils ont même hypoténuse, alors
ils sont superposables.
Un triangle
rectangle est DONC parfaitement déterminé par son hypoténuse
et par la mesure α de l'un de
ses angles non droits.
Son AIRE (sa surface),
Si l'on fixe la longueur c
de l'hypoténuse du triangle rectangle alors son aire, va simplement
dépendre de l'angle α.
L'aire est une fonction f(α).
Peu nous importe quelle est cette fonction (*),
on sait juste qu'elle ne dépend que de l'angle α.
Par ailleurs l'aire du triangle dépend du carré des
longueurs des côtés, donc du carré c²
puisque l'hypoténuse détermine
le triangle de façon unique si l'angle α
est fixé.
Ainsi
Aire(ABC) =
c² f(α)
| Découpons
(ABC) en deux triangles rectangles (ABH) et (CAH) en traçant
sa hauteur issue du point A, sommet de l'angle droit
Les deux petits triangles (ABH) et (CAH) ont le même angle
α en A
et C, car les côtés de ces angles sont perpendiculaires
deux à deux.
L'hypoténuse de (ABH) est
a ; L'aire de (ABH) est donc
a² f(α).
L'hypoténuse de (CAH) est b
; L'aire de (CAH) est donc b²
f(α).
On a vu que l'aire de (ABC) est c²
f(α).
On déduit :
c²
f(α) = a²
f(α) + b²
f(α)
D'où
c²
= a² + b²
|
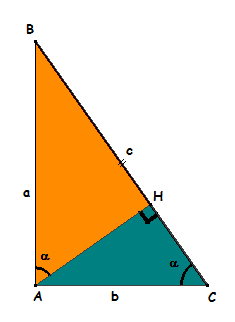 |
(*)
Cette fonction est la fonction trigonométrique de l'angle α
: 0.5*sin(α)
cos(α)
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
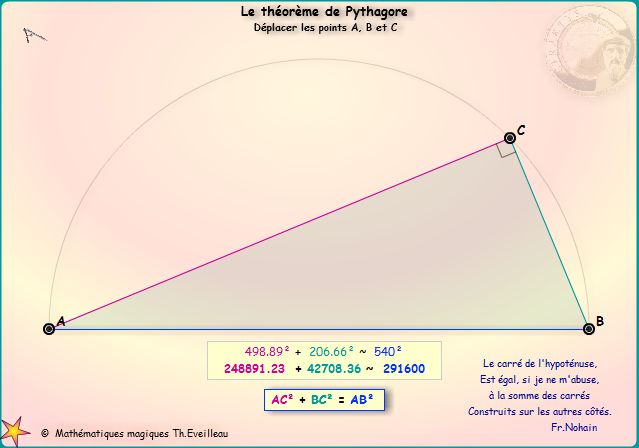
Démonstration
visuelle N°1
CLIQUER
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Démonstration
N°2
Traçons un triangle rectangle et sa hauteur issue
du sommet de l'angle droit.
Dans l'animation suivante, déplacer les points A puis B et
C.
CLIQUER

Les trois
triangles AHB, CHA et CAB sont semblables car ils ont
des angles de même mesure :
ils sont tous les trois rectangles et leurs angles aigus ont leurs
côtés respectivement perpendiculaires deux à deux.
Il s'ensuit que le rapport des mesures homologues est
identique pour les trois triangles.
C'est le cas pour le quotient de l'aire par le carré de l'hypoténuse
de chaque triangle.
.
Appelons
A1
l'aire du triangle d'hypoténuse a=AB, B1
l'aire du triangle d'hypoténuse
b=AC et C1
celle du triangle d'hypoténuse
c=BC.
Il vient :
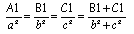
Cette dernière égalité est
une propriété que l'on retrouve avec un simple tableau
de proportionnalité,
dans lequel nous plaçons les aires sur la première ligne
et les carrés des hypoténuses sur la deuxième
ligne.
. Finalement :

Comme nous savons
que A1
=
B1 + C1,
nous en déduisons que
a²
= b² + c².
C'est bien la propriété
de Pythagore.
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
Démonstration
visuelle N°3
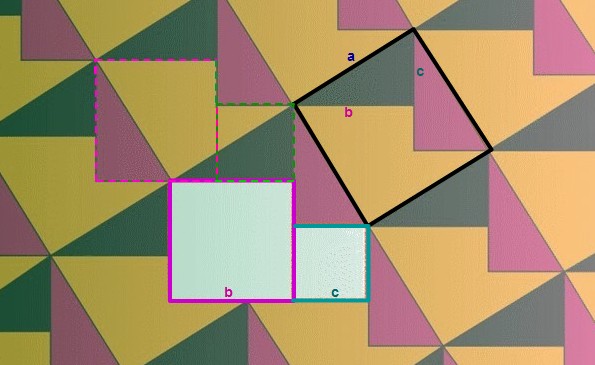
Observez bien le pavage ci-dessous qui me vient de P.Jullien.
Il
constitue également une très jolie démonstration
visuelle du théorème de Pythagore.
Les deux carrés
blancs de côtés respectivement
b
et c,
sont composés ensemble d'une pièce
jaune, d'une verte et d'une rose.
Il en est de même du carré oblique de côté
a.
Nous obtenons ainsi a²
= b²
+ c²
 Le
Théorème
de
Le
Théorème
de