Le
ballon dans son filet
Le
problème suivant vous est proposé par Diophante
(D346 octobre 2014)
Douze lacets de
même longueur sont noués entre eux à leurs extrémités
de manière à constituer un filet comportant huit noeuds
qui peuvent être placés sur les sommets d’un cube
d’arête a. On place un ballon sphérique à
l’intérieur du filet et on le gonfle de sorte que le
filet est parfaitement tendu sur sa surface.Le volume du ballon est
alors de 9200 cm3.
En déduire a.
L'animation
suivante permet de voir le filet puis le ballon gonflé.
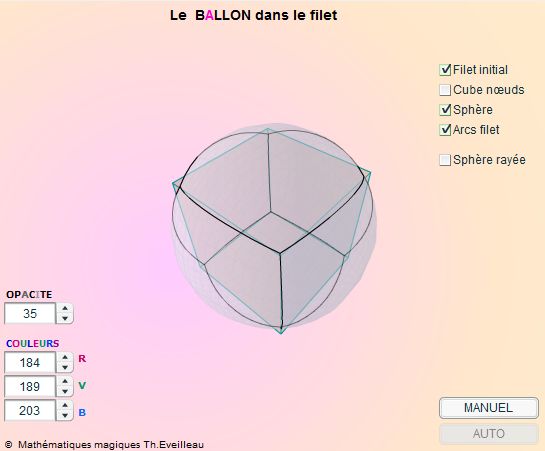
En cochant les boutons adéquats on peut voir
-le cube initial
aux arêtes vertes, correspondant au filet tendu par le ballon
gonflé, est constitué des douze lacets ;
-le cube aux arêtes rouges, intérieur au ballon dont
les sommets sont les nœuds du filet ;
-la sphère correspondant au ballon gonflé dont on peut
jouer sur la transparence et la couleur ;
-le filet tendu dessiné en noir, visible ou non à travers
le ballon, selon sa transparence.
Les arêtes vertes du grand cube ont la même longueur
que chaque arc tendu sur le ballon entre les nœuds.
En mode MANUEL
Il
est possible de faire tourner le ballon,
- soit avec les flèches du clavier : gauche et droite, haut
et bas et enfin les touches Ctrl et Maj
-soit en cliquant tirant la souris sur les objets.
Cliquer le bouton AUTO pour obtenir une rotation automatique.
CLIQUER
Solution rapide du problème
Très
rapidement, le volume de 9200
cm3 donne
un rayon de quasi 13 cm avec la formule
Volume = 4/3 π R3
.
Si
a est le côté du cube dont les sommets sont les nœuds
du filet, nous avons la relation :
R = a  /
2 .
/
2 .
On en déduit que a = 2 R
/ .
.
Avec un rayon de 13 cm, nous avons environ 15 cm comme longueur
d'arête du cube intérieur formé sur sur les
nœuds.
L'arc final du filet sur la sphère sous tend un angle dont
la moitié a pour sinus a/2R.
L'angle sous tendu par l'arc est d'environ
70.47 °.
La longueur de l'arc est donc 2πR *70.47/360 ~ 16 cm.
Différentes
solutions vous sont proposées chez Diophante ICI.

