L'étoile porte-bonheur
sur le casse-tête D206 d'avril 2016 de Diophante

---

Casse-tête d'avril 2016

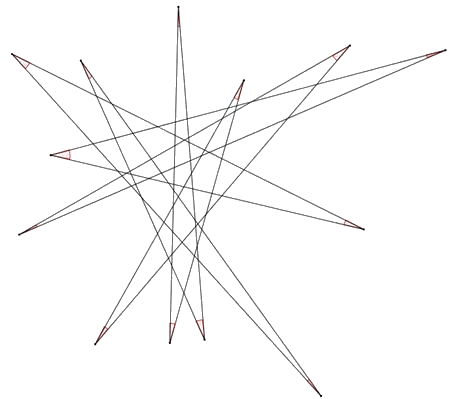
Il suffit de bien observer cette étoile à treize branches dans laquelle trois droites ou plus ne sont jamais concourantes afin de déterminer la somme des angles (marqués en rouge) des treize sommets.
C'est un casse-tête simple qui fait appel à quelques additions comme celui du mois dernier. Une seule recommandation, ne cherchez pas le millésime 2016 sous une forme ou sous une autre.

Solution
Voir le site de Diophante.fr pour diverses solutions et explications.

La somme est d'un demi-tour : soit π.

Nommons αi les angles en chacun des sommets.
J'imagine un animal allant d'un point vers un autre sur l'idée de la tortue Logo.
Quand la tortue arrive en chacun des sommets elle pivote de π- αi pour arriver sur chaque nouveau sommet.
On note d'ailleurs qu'elle tourne toujours dans le même sens (c'est la clé du problème).

Aussi quand elle revient au point de départ elle a fait un tour complet, donc un angle multiple de 2π.
Ainsi nous avons en sommant sur i de 1 à 13 :
(π - αi ) congru à 0 modulo 2π .
Il faut donc que 13π - αi soit égal à π.

La somme des angles de ce polygone de 13 sommets est égale à π.
Ceci est valable pour tout polygone ainsi construit avec un nombre impair de sommets.
Le triangle est un cas spécial.

 

 

CLIQUER