Le problème

Uniquement avec des ciseaux, à l'aide de plis, mais sans rien mesurer, découper un carré de papier, pour fabriquer très exactement 5 carrés identiques.
Autre problème : comment partager une pizza carrée en cinq carrés identiques avec un couteau ?



L'animation

Un carré, quatre segments menés de chacun des sommets vers le milieu d'un côté... et voici comment obtenir 5 carrés identiques dans le carré initial.

 

CLIQUER

Maintenant, fabriquez votre puzzle : avec les cinq carrés... reconstituez un seul grand carré.

Démonstration

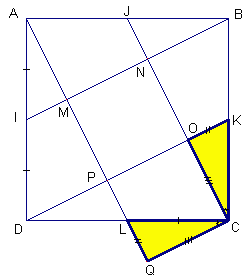
Les huit segments [AJ], [JB], [BK], [KC], [CL], [LD], [DI] et [IA] sont de même longueur comme moitiés du côté du carré ABCD. Le triangle KCD se déduit du triangle JBC par rotation de 90°. Les deux côtés homologues [JC] et [KD] sont donc perpendiculaires et le triangle KOC est rectangle. Par une rotation de 270° dans le sens des aiguilles d'une montre, le triangle OKC devient QLC puisque LC=KC=AB/2. L'angle OCQ est droit : 360°-270°. Les points P, L et Q sont alignés car l'angle QLC égale l'angle PLD (cela vient de l'égalité des triangles DPL et COK). POCQ est un rectangle avec deux côtés consécutfs de même mesure, c'est donc un carré. Autour du carré ABCD nous obtenons ainsi quatre carrés superposables ( constitués d'un trapèze rectangle auquel on a adjoint un triangle rectangle (exemple : NBKO et OKC)). De la même façon que nous avons obtenu par rotation, la perpendicularité de [JC] et [ DK] nous avons celle de [AL] et [ DK] puis celle de et [IB] et [ AL] et enfin celle de [JC] et [ IB]. MNOP est un rectangle et pour raison de symétrie c'est un carré. A partir de PO=OC, on démontre que les côtés de MNOP sont de même mesure que ceux du carré POCQ.

FINALEMENT, nous avons décomposé ABCD en 5 carrés superposables à MNOP.
L'aire de ABCD est donc égale à 5 fois celle de MNOP.

AB = MN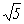

On note également que IB =2,5 MN
En effet, PO=OC=DP
et PO=PL+LQ=2LQ=2OK d'où OK=0,5 PO
donc DK= 2,5 PO et de même IB=2,5 MN.

Remarque :
AJCL est un parallélogramme car ses côtés [AJ] et [LC] sont à la fois de même mesure et parallèles.
On démontre alors simplement que BJ = AB/2 en utilisant la réciproque du théorème de la droite des milieux dans le triangle ABM :
en effet (JN) // (AM) et J milieu de [AB] implique que
(JN) est la droite des milieux et que
N est le milieu de [BN] et aussi que
JN = AM/2.

Autre démonstration rapide plus visuelle
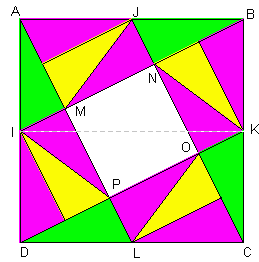
On peut tracer les parallèles suivantes
la parallèle à (MN) passant par J ;
la parallèle à (MP) issues de I ;
la parallèle à (OP) issue de L ;
la parallèle à (ON) issue de K.
Les triangles colorés sont superposables (triangles semblables ayant au moins un côté de même longueur).
Nous obtenons 16 triangles superposables au triangle BJN.