Les deux cibles

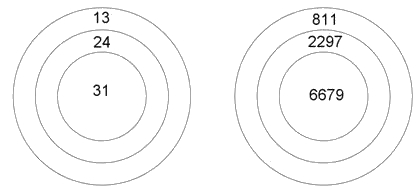
Le problème des deux cibles *****    
il s'agit du n° A2994 dans Diophante.fr



Q1 Sur la première cible, le disque central vaut 31 points, la couronne intermédiaire 24 points et la couronne externe 13 points.
Déterminer le plus grand total entier impossible à atteindre.
Q2 Sur la deuxième cible, les nombres affichés dans le disque central, la couronne intermédiaire et la couronne externe sont 811, 2297 et 6679.
Déterminer le plus grand total entier impossible à atteindre.

Ce problème est difficile si l'on veut le généraliser.
Source de Q1: problème n°16 de la finale suisse du championnat des jeux mathématiques 2018.


ANIMATION et résultats

Dans l'animation les nombres entrés doivent être premiers entre eux deux par deux.


Entrer les nombres et suivre les consignes de l'animation suivante.

 

PLEIN ECRAN


Voir différentes solutions ici :
http://www.diophante.fr/problemes-par-themes/arithmetique-et-algebre/a2-algebre-elementaire/4237-a2994-les-deux-cibles

Pour une explication dans le cas particulier demandé, je recommande vivement la solution magique et concise de Pierre Palmade.


Ce problème est difficile… apparemment connu sous le nom du rendu des pièces de monnaie ou le problème de Frobenius number.

J’ai programmé cette animation avec l’algorithme de Rödseth de ce document :
https://etd.auburn.edu/bitstream/handle/10415/273/TRIMM_JANET_47.pdf;sequence=1

Menu trucs  Accueil