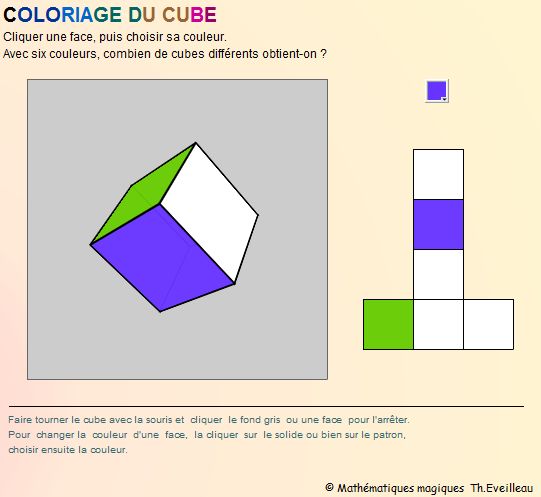
On veut colorier un cube en utilisant six couleurs différentes.
Toutes les faces sont de couleur différente.
Deux cubes sont identiques s'ils le sont à une rotation près.
Combien de cubes différents obtient-on ?


Dans l'animation suivante
- on arrête la rotation du cube en cliquant soit le cube soit le fond gris ;
- après avoir cliqué une face du patron ou du cube, choisir une couleur pour colorier la face choisie.
Attention un même cube peut avoir des patrons différents...

CLIQUER

 

 

SOLUTION

Avec six couleurs et en utilisant chaque couleur une seule fois, nous trouvons 30 cubes différents aux rotations près. Exemple de raisonnement Choisissons de colorier la face de gauche G, puis son opposée D. Nous avons 5 possibilités pour la face D. Restent 4 couleurs pour les 4 faces de la bande H K L C. Si l'on confond une face avec sa couleur pour simplifier, nous avons les possibilités : HKLC (donnant le même cube que KLCH ou LCHK ou CHKL en faisant une rotation) HKCL HLKC HLCK HCKL HCLK Nous avons donc 6 possibilités. Finalement cela donne 5 x 6 = 30 possibilités.

Et avec 7 couleurs ?

Nous devons pour chaque cube choisir 6 couleurs parmi 7 (ce qui revient à choisir une couleur parmi 7).
Il y a 7 possibilités.
Pour chaque choix de 6 couleurs nous venons de voir qu'il y 30 façons de colorier le cube.
Ainsi pour 7 couleurs données, le nombre de cubes est multiplié par 7.
Finalement avec 7 couleurs, nous obtenons 30 x 7 = 210 cubes différents.

---