Peavages d'hexagones, problème D4901 *** avec Diophante.fr

Avec n triangles équilatéraux de côté unité, on pave un hexagone pas nécessairement convexe dont les côtés ont pour longueurs pas nécessairement prises dans cet ordre 1, 2 ,3 ,4 ,5 , 6.
Q1 Démontrer que l'entier n est toujours impair.
Q2 Déterminer les valeurs extrêmes de n et représenter les pavages correspondants.
Pour les plus courageux :
Q3 Déterminer toutes les valeurs possibles de n.
Q4 Déterminer tous les pavages possibles non superposables deux à deux.


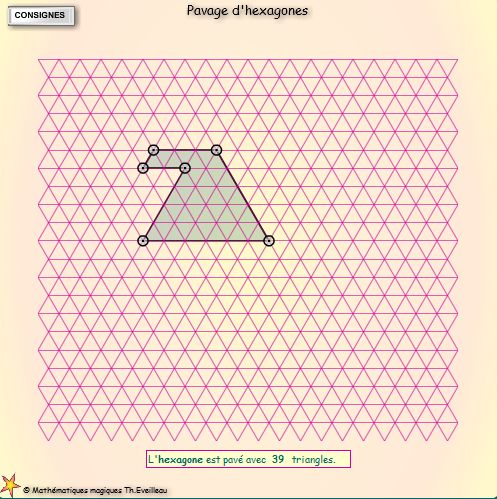
ANIMATION

L’animation suivante permet d’expérimenter et de construire rapidement les hexagones comme sur une feuille triangulée sans gomme ni crayon. Les nombres de triangles sont automatiquement calculés.
Quand le polygone ‘passe au vert’ il est OK si non croisé.

SOLUTION

Q1

Nous avons 3n côtés pour ces triangles.
Tous les côtés sur le tour de l’hexagone sont comptés 1 fois (il y en a 21), les k autres intérieurs strictement au polygone, sont comptés deux fois.
Ainsi 3n = 21 + 2k.
Donc 3n est impair, ce qui implique que n est impair.

Q2

Les extrêmes sont :
25 triangles équilatéraux et 67 triangles équilatéraux.

 

Q3

Les valeurs possibles de n sont les suivantes :
25, 27, 29, 31, 33, 35, 37, 39, 43, 45, 51, 53, 55, 57, 65 et 67.

Q4

Et voici différentes solutions.

Voir la page de Diophante avec différentes propositions de solutions