Une convexité
très probable ?
LE PROBLÈME
www.diophante.fr
le n° G1909
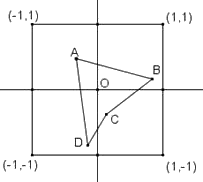On choisit
au hasard quatre points A,B,C,D indépendamment les uns des
autres,
dans les quadrants respectifs Nord Ouest, Nord Est, Sud Est et Sud
Ouest d’un carré dont les sommets ont pour
coordonnées (–1,1), (1,1),(1, –1) et (–1,
–1)
Est-il exact que la probabilité que le quadrilatère
ABCD soit convexe est supérieure à 90% ?
ANIMATION
-On peut JOUER et observer calmement...
Le bouton STOPPER arrête le jeu
et établit score et moyenne sur l'ensemble des jeux.
-On peut faire une SIMULATION rapide ou évolutive
selon le nombre jeux.
La stratégie repose sur le nombre de cases à
clliquer, au-delà duquel on arrête de jouer avec le bouton
STOPPER.
-Entrer au clavier ou avec les flèches
les valeurs pour le nombre de jeux (expériences).
/!\ ATTENTION
si les données sont entrées au clavier, VALIDER
ensuite avec la touche ENTREE.
Le mode Ultra RAPIDE donne immédiatement
le résultat de la simulation.
Le bouton RAZ permet de recommencer le
jeu individuel en remettant le nombre de jeux à 0.
Le curseur vitesse permet de modifier la vitesse d'exécution.
CLIQUER
ANALYSE
La réponse est oui avec une probabilité d'environ 90.91%.
L'animation donne ce résultat avec un très nombre d'expériences.
Pour
une belle démonstration complète avec Diophante astucieuse
et simple mais en anglais aller ici :
http://stanwagon.com/public/1305FondanaicheSolution.pdf
et
encore
www.diophante.fr le n° G1909
