Les
parcours platoniciens de la coccinelle et de la fourmi
Deux insectes se baladent sur un icosaèdre et un dodécaèdre.
"La vie c'est une boîte de chocolats, on ne sait jamais sur quoi on va tomber". Forrest Gump 1994
___________
Le
problème
G194 Parcours platoniciens***
avec Diophante.fr
Deux structures
métalliques qui ont respectivement la forme d'un icosaèdre
régulier et d'un dodécaèdre régulier sont
suspendues à un fil par l'un de leurs sommets. Les deux structures
s'inscrivent dans des sphères de même rayon égal à
30 cm.
Coccinella Septempunctata est installée au sommet le plus haut
de la première et Formicida Lasius Niger au sommet le plus haut
de la deuxième.
Les deux bestioles décident au même moment de se promener
en suivant les arêtes de leur habitacle,la coccinelle à la
vitesse uniforme de 20 cm par minute et la fourmi à la vitesse
uniforme de 32 cm par minute. Chaque fois que l'une ou l'autre arrive
à un sommet, elle choisit l'une quelconque des arêtes qui
partent de ce sommet avec une égale probabilité, quitte
à faire marche arrière. Quand elles parviennent au sommet
le plus bas, elles s'arrêtent pour faire une pause avant de recommencer
une nouvelle promenade.
Déterminer l'écart (en minutes et secondes) qui sépare
la durée moyenne de leurs parcours.
ANIMATION
avec les solides 3D
___________
La même animation
est réalisée en bas de la page,
avec des déplacements visualisés sur un graphe planaire.
Note
sur la représentation et les vitesses et durées réelles
Pour des raisons évidentes, les durées des déplacements
sont modifées pr rapport au temps réel.
Cependant, les proportions entre les
durées et les déplacements sont rigoureusement respectées.
Ainsi, dans
la représentation, les arêtes ne paraissent pas isométriques.
MAIS elles le sont dans la réalité.
Aussi dans les deux animations, la durée du parcours d'une arête
est constante quelle que soit sa longueur sur la représentation
'aplanie'.
C'est ainsi que l'on peut observer des accélérations,
selon la longueur apparente de ces arêtes.
- Lorsque
le bouton ' simulation insectes
' est coché,
--> on peut suivre les déplacements, arête
par arête de chacun des deux insectes sur son polyèdre.
- Lorsque ce même bouton
est décoché,
--> on peut obtenir les résultats très rapidement
pour de nombreux parcours (jusqu'à 50 000).
Nous obtenons alors une bonne espérance
pour les nombres d'arêtes parcourues et la durée
des parcours.
- Choisir le nombre d'expériences à réaliser pour
obtenir. Plus le nombre est grand et plus les résultats sont significatifs.
- On peut modifier la vitesse d'exécution.
Cela ne modifiera pas les durées réelles des
parcours. Seule l'exécution sera plus ou moins rapide.
ATTENTION : penser
à appuyer la touche ENTREE après avoir modifié le
nombre d'expériences.
CLIQUER
SOLUTION et EXPLICATION
Je vais découper
chaque solide par niveaux :
-> 0 le sommet, 1 le suivant…
-> Nous avons 3 niveaux pour l’icosaèdre et 5 niveaux
pour le dodécaèdre.
Icosaèdre et coccinelle avec une vitesse de 20 cm par minute
Soit Pn
, le nombre d’arêtes parcourues en moyenne par la coccinelle
pour aller du niveau n, vers le bas de l’icosaèdre.
Pour chaque niveau, la coccinelle a une chance sur 5 de passer d’un
sommet à l’un de ses voisins.
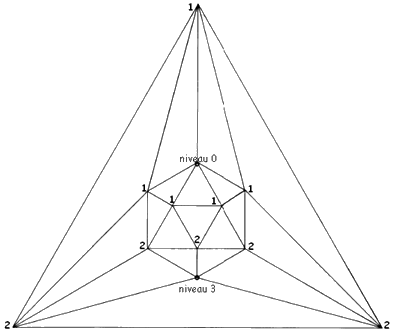
Graphe planaire de l’icosaèdre
Le niveau 0 représente le haut de l’icosaèdre
et
|
p0
= 1 + 1/5 (5 p1)
= 1 + p1 |
Icosaèdre et coccinelle avec une vitesse
de 20 cm par minute
Mêmes notations
que précédemment.
Pour chaque niveau, la fourmi a une chance sur 3 de passer d’un
sommet à l’un de ses voisins.
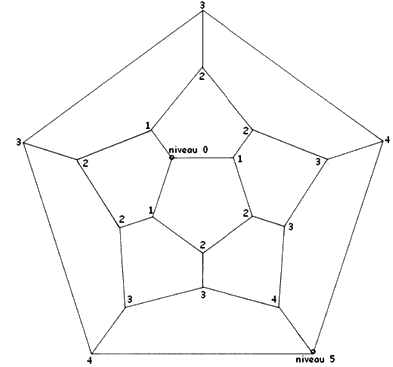
Graphe planaire du dodécaèdre
Le niveau 0 représente le haut de l’icosaèdre
et
|
p0
= 1 + 1/3 (3p1)
= 1 + p1 |
La différence entre les deux est d’un peu plus de 14 secondes.
ANIMATION
avec les solides représentés à l'aide d'un graphe
planaire
_____________
(1)
CLIQUER
Un peu plus avec Diophante.fr