|
Les
triangles obtus construits sur un polygone régulier
Ce
problème est le n° G2927 de
Diophante.fr
On choisit au hasard trois sommets d'un polygone régulier de
n côtés. Pour quelles valeurs de n, a-t-on exactement une
chance sur deux d'obtenir les sommets d'un triangle obtus ?
SOLUTION
Les seules possibilités
sont le pentagone et le dodécagone.
Une modélisation animée et interactive permet de visualiser
ces résultats.
La démonstration générale est traitée juste
après les exemple et l'animation.
Etudions quelques exemples
Nous numéroterons les sommets du pentagone de 0 à (n-1)
en tournant dans le sens des aiguilles d’une montre.
-Pour un polygone régulier de 4 côtés
on a une probabilité de 0%.
Les carrés ne sont
donc pas retenus.
-Pour un polygone
régulier de 5 côtés on a 50%
de chances.
En effet, il y a 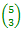 =
10 possibilités de construire un triangle dont les sommets sont
des sommets du pentagone. =
10 possibilités de construire un triangle dont les sommets sont
des sommets du pentagone.
Dans ces triangles sont obtus seulement ceux qui ont trois sommets consécutifs
du pentagone avec un angle de 108°.
Ces triangles sont au nombre de 5.
Nous avons donc 5 chances sur 10 soit exactement 50% de chances.
Les pentagones réguliers
sont retenus comme solution du problème.
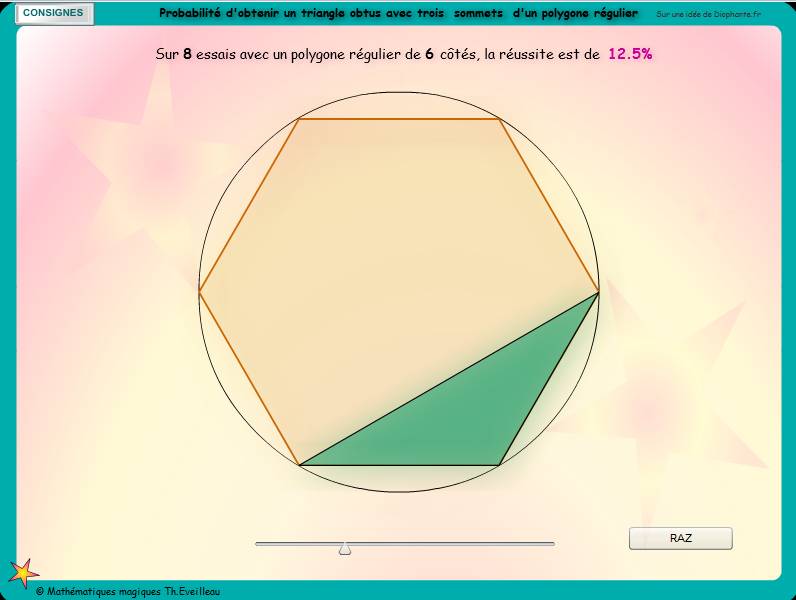
-Pour un polygone
régulier de 6 côtés on a environ
30% de chances.
En effet, il y a  = 20 possibilités de construire un triangle dont les sommets
sont des sommets du pentagone.
= 20 possibilités de construire un triangle dont les sommets
sont des sommets du pentagone.
Dans ces triangles on retient ceux qui ont 3 sommets consécutifs
(angle de 120°).
Ces triangles sont au nombre de 6.
Les autres sont soit rectangles soit avec trois angles aigus.
Donc nous avons 6 chances sur 20 soit une probabilité de 30%.
Les hexagones réguliers
ne sont pas retenus.
-Pour un polygone
régulier de 7 côtés on a 60% de
chances.
En effet, il y a  =
35 possibilités de construire un triangle dont les sommets sont
des sommets du pentagone. =
35 possibilités de construire un triangle dont les sommets sont
des sommets du pentagone.
Dans ces triangles on retient ceux qui ont 3 sommets consécutifs
(angle de 128.5°).
Ces triangles sont au nombre de 7.
Avec un angle de 128.5° - (180°- 128.5°) / 2 = 102.75°
Retenons les 14 triangles ayant deux sommets consécutifs et deux
autres séparés par un sommet du polygone régulier
:
triangles (4,6,0) ; ( 5,0,1) ; (6,1,2) ; (0,2,3) ; (1,3,4) ; (2,4,5)
; (3,5,6) ;
ET les triangles (0,1,3) ; (1,2 4) ; (2,3,5) ; (3,4,6) ; (4,5,7) ; (5,6,1)
; (6,0,2).
Donc nous avons 21 chances sur 35 soit une probabilité de 60%.
Les heptagones réguliers
ne sont pas retenus.
-Pour un polygone
régulier de 8 côtés on a une probabilité
d’environ 42.8 %.
En effet, il y a  =
56 possibilités de construire un triangle dont les sommets sont
des sommets du pentagone. =
56 possibilités de construire un triangle dont les sommets sont
des sommets du pentagone.
On retient les triangles ayant 3 sommets consécutifs avec un
angle de 135°.
Ces triangles sont au nombre de 8.
Ceux ayant
deux sommets consécutifs, le troisième ayant un décalage
de deux avec l’un d’entre eux (angle de 112.5°).
Exemples : (0,1,3) ; (1,2,4) ;
Lorsque 2 sommets consécutifs sont choisis, il reste deux possibilités
pour le troisième sommet.
Choisir deux sommets consécutifs parmi 8 revient à choisir
1 sommet parmi 8.
Donc nous aurons 8*2 = 16 triangles ainsi construits.
En tout nous obtenons 16 + 8 soit 24 triangles obtusangles.
On a finalement 24 / 56 soit une probabilité de ~ 42.8 %.
Les octogones réguliers
ne sont pas retenus.
-Pour un polygone
régulier de 9 côtés on a environ
64.5% de chances.
En effet, il y a 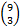 = 84 possibilités de construire un triangle dont les sommets
sont des sommets du pentagone
= 84 possibilités de construire un triangle dont les sommets
sont des sommets du pentagone
On retient les triangles ayant 3 sommets consécutifs avec un
angle de 140°.
Ces triangles sont au nombre de 9.
On retient les triangles ayant 2 sommets consécutifs et un décalé
de deux sommets avec un angle de 120° comme (0,1,3) .
Lorsque 2 sommets consécutifs sont choisis, il reste deux possibilités
pour le troisième sommet.
Il y a donc 9 *2 = 18 cas.
On retient enfin les triangles ayant 2 sommets consécutifs et
un décalé de trois sommets avec un angle de 100° comme
(0,1,4).
Même résultat : 9*2 = 18 cas.
Et enfin les triangles isocèles avec chacun des sommets décalés
de 2 et un angle de 100°.
Il y en autant que de sommets du polygone : 9.
On a finalement une probabilité de (9+18 +18 +9) / 84 = 54 /
84 soit une probabilité d’environ 64.28%.
Les ennéagones réguliers
ne sont pas retenus.
-Pour un polygone
régulier de 10 côtés on a 50% de chances.
En effet, il y a 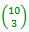 =
120 possibilités de construire un triangle dont les sommets sont
des sommets du pentagone. =
120 possibilités de construire un triangle dont les sommets sont
des sommets du pentagone.
On retient les triangles avec trois sommets consécutifs et un
angle de 144°.
Ces triangles sont au nombre de 10.
Comme ci-dessus les triangles comme (0,1,3) (angle de 126°). Il
y en a 10*2 = 20.
Les triangles comme (0,1,4) (angle de 108°). Il y en a 10*2 = 20.
Les triangles isocèles comme (0,2,8) (côtés décalés
de 2 avec un angle obtus de 108°). Il y en a exactement 10.
On a finalement une probabilité de (10+20+20+10) / 120 = 50%
Les décagones réguliers
sont retenus comme solution du problème.
Le décagone
et le pentagone répondent à la question.
L'animation
-Lire
les consignes en posant et en laissant le curseur souris sur le bouton
CONSIGNES.
-Moduler éventuellement la vitesse d'exécution en déplaçant
le curseur vitesse.
-Taper
le nombre de côtés du polygone régulier.
-Taper le nombre d'expériences désirées.
CLIQUER
Généralisation
et démonstration avec
un polygone régulier de n côtés
Chaque angle d’un polygone régulier de n côtés
mesure (180 - 360/n)° soit 180*(n-2) / n degrés.
Nombre de cas possibles
On aura 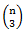 = n(n-1)(n-2)/6 cas possibles pour construire
un triangle dont les sommets sont des sommets du polygone.
= n(n-1)(n-2)/6 cas possibles pour construire
un triangle dont les sommets sont des sommets du polygone.
Nombre
de cas favorables
Nous aurons les triangles obtus (0,1,3)… au nombre de 2n.
Nous aurons les triangles obtus (0,1,4)… au nombre de 2n.
Les triangles obtus (0,1,5)… au nombre de 2n.
Tous
conviennent car l’un des angles est plus grand que 90° (limite
obtenue lorsqu’un côté devient l’axe de symétrie
de la figure, le triangle inscrit alors un demi-cercle).
…
Les triangles (0, 2, (n-2)) etc. sont au nombre de n.
Probabilité
= nombre de cas favorables / nombre de cas possibles.
Si n
est pair
Si
n = 4 -> 4*0 cas favorables soit 0
Si n = 6 -> 6*1 cas favorables soit 6.
Si n = 8 -> 8(1+2) = 8*3 cas favorables soit 24.
Si n = 10 ->10(1+2+3) = 10*6 cas favorables soit 60.
Si n = 12 ->12(1+2+3+4) = 12*10 cas favorables soit 120
.
.
.
Finalement
n=10 est solution unique si n est pair.
Si n est impair
Si
n = 5 -> 5*1 = 5 cas favorables .
Si n = 7 -> 7(1+2) = 21 cas favorables.
Si n = 9 -> 9(1+2+3) = 54 cas favorables.
.
.

Finalement
n=5 est solution unique si n est impair.
Notons que
lorsque n croît la probabilité tend vers 75%.
|
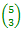 =
10 possibilités de construire un triangle dont les sommets sont
des sommets du pentagone.
=
10 possibilités de construire un triangle dont les sommets sont
des sommets du pentagone. = 20 possibilités de construire un triangle dont les sommets
sont des sommets du pentagone.
= 20 possibilités de construire un triangle dont les sommets
sont des sommets du pentagone. =
35 possibilités de construire un triangle dont les sommets sont
des sommets du pentagone.
=
35 possibilités de construire un triangle dont les sommets sont
des sommets du pentagone. =
56 possibilités de construire un triangle dont les sommets sont
des sommets du pentagone.
=
56 possibilités de construire un triangle dont les sommets sont
des sommets du pentagone.

