|
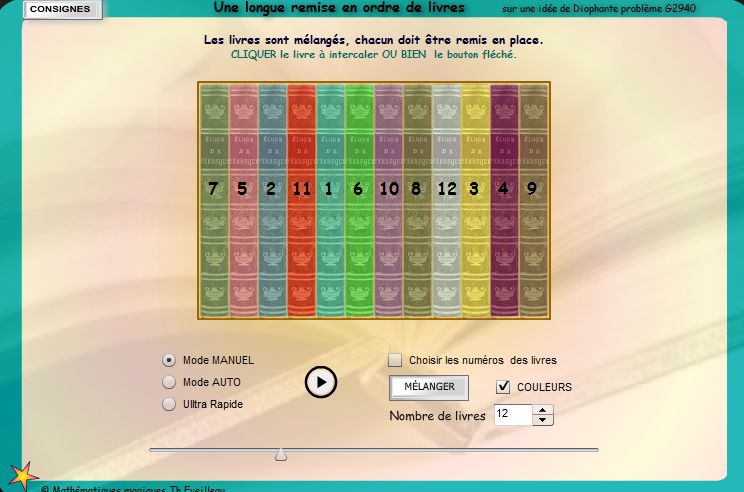
Le problème STRATÉGIE à choisir et ANIMATION LE PLUS LONG RECLASSEMENT et ANIMATION ANALYSE et résultats "Nul ne peut être un mathématicien accompli s'l n'a pas l'âme d'un poète." KARL WEIERSTRASS, LETTRE à SOPHIA KOVALEVSKAYA, 1883. Le problème Sur l'idée du G2940 de Diophante.fr Zig a sur une étagère de sa bibliothèque une collection de n ouvrages mathématiques qu'il a étiquetés et rangés de 1 à n.En son absence, Puce mélange l'ordre des ouvrages. A son retour Zig demande à Puce de remettre les volumes dans le bon ordre, c'est à dire de gauche à droite : 1,2,..n , et lui impose le processus suivant : si l'ouvrage étiqueté n° k est à droite de la position n° k, alors cet ouvrage est placé en position n°k. Par exemple, si l'étagère contient dans cet ordre les ouvrages 4,1,3,2, Puce prend soit l'ouvrage n°1 qu'il place en première position et l'ordre des ouvrages devient 1,4,3,2 soit l'ouvrage n°2 qu'il place en deuxième position et l'ordre des ouvrages devient 4,2,1,3. Q1 Démontrer que Puce est certain de remettre la totalité des ouvrages dans le bon ordre en un nombre fini d'étapes quel que soit le choix de l'ouvrage à reclasser à chacune de ces étapes. Q2 Déterminer le plus grand nombre possible d'étapes que le processus peut demander quand à chaque étape on prend l'ouvrage qui se trouve le plus à droite des ouvrages à reclasser. Application numérique n = 20. Temps de reclassement d'un ouvrage: 3 secondes. Déterminer le temps total maximum de la remise en ordre.
ANIMATION
avec
la procédure de la question Q1
:
une certaine liberté
dans le choix de l'ouvrage à prendre. ANIMATION
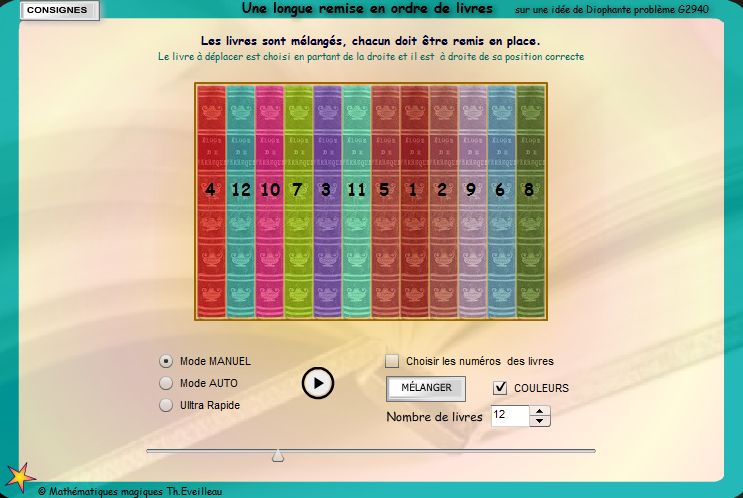
sur
la question Q2
: TROUVER le plus long RECLASSEMENT.
Très vite, on peut observer que le nombre maximal d'étapes est obtenu avec la stratégie de la deuxième partie. Le
temps de rangement peut devenir très grand lorsque les ouvrages
sont classés d'une certaine façon. Essayer
de faire un maximum d'observations avant d'aller ci-dessous ou ICI chez
Diophante.fr pour en savoir un peu plus.
|