|
Le
problème
Une
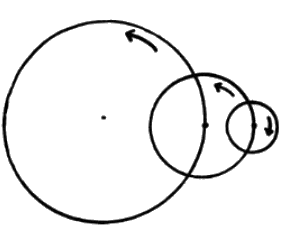
grande roue tourne dans un sens, une deuxième plus petite,
dont le centre est fixé sur la circonférence de
la plus grande roue, tourne plus rapidement dans le même
sens.
Enfin une troisième roue, dont le centre est fixé
sur le pourtour de la deuxième, tourne en sens inverse.
On fixe une nacelle sur le tour de la troisième roue.
Vertigineux ! Il s'agit là de la roue de Ferris.
Quelle est la trajectoire de la roue ?
Dans l'exemple proposé, le rayon de la grande roue est
1 ; celui de la deuxième 1/2 et celui de la troisième
1/3.
La deuxième roue tourne en apparence 7 fois plus vite
que la grande dans le même sens.
La troisième tourne 17 fois plus vite que la première
en sens inverse.
Curieusement, le chemin parcouru par la nacelle présente
une belle symétrie d'ordre 6. Inattendu, non ?
|
 |
Question
Quel est le chemin
parcouru par le passager de la nacelle ?
Quelles courbes obtiendrons-nous avec d'autres vitesses et d'autres sens
de rotation ?
Comment obtenir des
courbes présentant de belles symétries ?
L'animation ci-dessous permet d'analyser la situation.
On peut changer les paramètres dès lors que les roues
sont au repos.
ANIMATION
. Ne pas hésiter à
modifier les différentes valeurs des paramètres.
. Les vitesses de ROTATION sont
entrées au clavier : chaque case prend la couleur de la roue
concernée.
-> Grande roue entre -5 et +5
-> Autres roues entre -30 et +30
. La phase indique le décalage
de la nacelle par rapport à l'horizontale dans le sens horaire.
. Les autres boutons sont explicites,
les cocher ou décocher : le fait de 'cacher' les roues permet
d'isoler le parcours de la nacelle.
. Pour voir la trajectoire de la
nacelle, cocher le bouton Trace du parcours.
. Pour le plaisir, varier les couleurs
en utilisant les boutons carrés colorés.
. La vitesse de rotation est également
modulable avec le curseur horizontal de vitesse.
Bon
voyage dans l'espace...
!
|

 PLEIN
ECRAN
PLEIN
ECRAN