CLIQUER

COMMENTAIRES et
SOLUTION
La
roue de Ferris, a été construite pour la première
fois à l'exposition universelle de Chicago en 1893.
Elle a été conçue par l'ingénieur spécialiste
des ponts George Ferris, qui était un expert en étais,
poutres et supports.
Cette roue a coûté 380 000 $ pour sa construction. Elle
mesurait 80m de hauteur.
Elle était constituée de deux moteurs à vapeur
et pouvait supporter 2 160 personnes.
Elle contenait 36 nacelles de 60 places chacune (places assises ou
debout).
De nombreuses évolutions de cette roue ont vu le jour depuis
: la nacelle n'est plus cantonnée au seul périmètre
de la roue...
Elles peuvent être aujourd'hui constituées deplusieurs
roues reliées par des bras hydrauliques
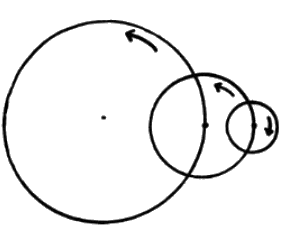
Frank A. Farris :
"I was thinking of the curve traced by a particleon a whhel
mounted on a wheel mounted on a wheel, each turning at a different
rate.
The first term represents the largest wheel, of radius 1, turning
counter-clockwise at one radian per second.
The second term represents a smaller wheel centered atthe edge of
the first, turning 7 times as fast.
The third term is for the smallest wheel centered atthe edge of the
second, turning 17 times as fast as the first, clockwise and out og
phase.
This curve displays a 6-fold symmetry, a fact that one would not guess...
"
FARRIS,
Frank A. "Wheels on wheels on wheels-Surprising
Symmetry."
Mathematics Magazine 69, N° 3(1996) : 185-189.
Courbes
mathématiques
Pour
comprendre cette partie mathématique,
il est indispensable de maîtriser le cercle
trigonométrique et les notions de cosinus et sinus (ICI).
Nous prendrons comme origine des coordonnées (0,0), le centre
de la plus grande roue.
Le centre de la deuxième est un point du pourtour de la grande
roue.
Soit t un instant donné depuis le début de la rotation
de la grande roue.
Soit a la vitesse de la première roue, b celle de la seconde
et c celle de la troisième roue.
Soit θ l'angle de décalage de la nacelle : le déphasage.
Le rapport des rayons est ici 1 ; 0.5 et 1/3.
Les coordonnées de la nacelle
sont :
x(t) = cosinus(a * t) + 0.5 *cosinus(b*t)
+ (1/3) * cosinus(c*t + θ )
y(t) = sinus(a * t) + 0.5 *sinus(b*t) + (1/3) * sinus( c*t+ θ
)
Pour ceux
qui connaissent les nombres complexes :
x(t) + i y(t) = e a
*it
+
0.5 * e i *b*t +
(1 /3) * e i*( c*t + θ)
SYMÉTRIE de la courbe
Si lorsque la valeur
de t augmente de &pi/n, nous retombons sur le même angle, nous
obtenons une symétrie d'ordre n.
Par exemple avec a = 1, b=7 et c=-17
Ces trois nombres ont le même reste dans la division par 6.
a=1 a pour reste 1 dans la division
par 6.
b=7 a pour reste 1 dans la division
par 6.
c=-17 a
même reste que -17+6+6+6 =1 dans la division
par 6. Donc c=-17 a pour reste 1 dans
la division par 6.
AINSI quand t augmente
de un sixième de tour, chaque roue a effectué un certain
nombre de tours entiers plus un sixième du tour suivant.
Au
bout d'un tour complet, chaque roue aura effectué six fois
le même chemin.
De façon générale, si a, b et c ont le
même reste dans la division par l'entier m, premier avec a,
b et c,
alors la courbe présente une symétrie d'ordre m.
Pour en savoir plus mathématiquement, voir
le texte en anglais de Frank A.Farrisici :
Wheels
on Wheels on Wheel-Surprising Symmetry
APPLICATIONS
Dans
le cas du problème, l'équation de la trajectoire est
:
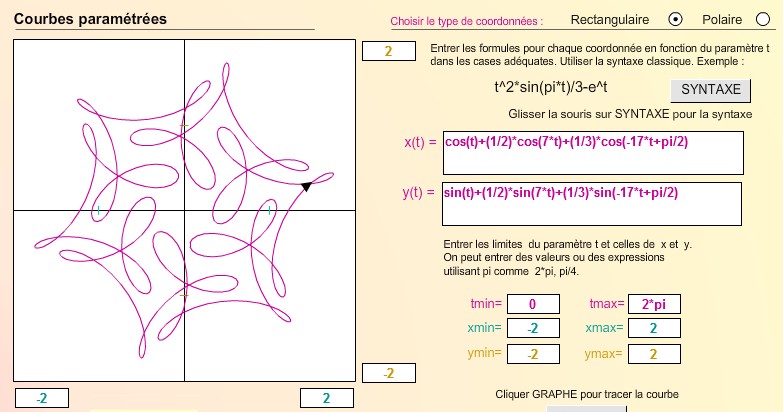
x(t) = cosinus(t) + 0.5 *cosinus(7*t) + (1/3) * cosinus(-17*t + π/2
)
y(t) = sinus(t) + 0.5 *sinus(7*t) + (1/3) * sinus(-17*t + π/2 )
qui deviennent si l'on préfère :
x(t) = cosinus(t) + 0.5 *cosinus(7*t) + (1/3) * sinus(17*t )
y(t) = sinus(t) + 0.5 *sinus(7*t) + (1/3) * cosinus(17*t )
Exemples
1, 7, -17 -> donne
une symétrie d'ordre 6 ;
-2, 5, 19 -> donne une symétrie d'ordre 7
;
1, -15, 17 -> donne une symétrie
d'ordre 16.
Voici les courbes graphiques obtenues ICI
et les équations mentionnées ci-dessus.
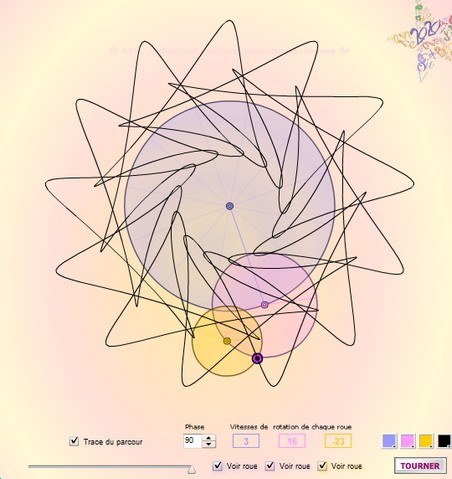
Avec les vitesses de rotation :
1 ; 7 ; -17 et une phase de π/2 -> symétrie
d'ordre 6.
OU
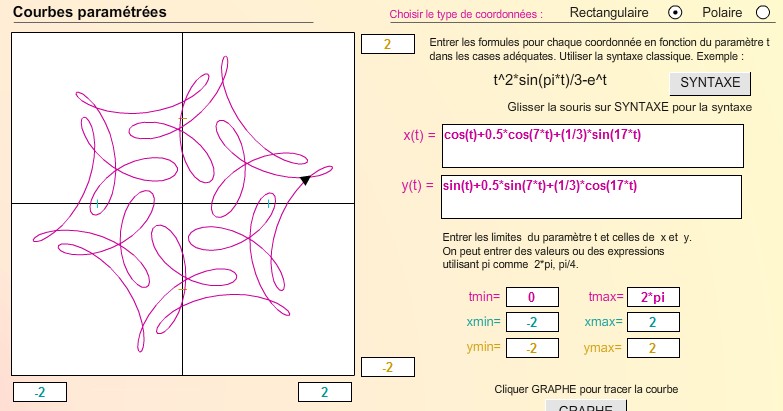
Avec les vitesses de rotation :
1 ; -15 ; 17 -> symétrie d'ordre 16.

Avec
les vitesses de rotation : 3 ; 8 ; -7 ->
symétrie d'ordre 5.

Avec les vitesses de rotation : 3 ; 16 ; -23 ->
symétrie d'ordre 13.