Le problème proposé par Pierre Jullien

Trois arbres binaires infinis possèdent une même racine et des troncs, de même longueur, à 120° les uns des autres.
De chaque nœud partent, à 120°, deux branches de même longueur égale à k fois la longueur de la branche qu'elles prolongent
(k fixe inférieur à 1).

Montrer qu'il existe une valeur K telle que si k < K les arbres sont disjoints et si k > K les arbres se chevauchent.


ANIMATION

- CHOISIR la valeur du rapport des longueurs des branches : la précision est de 1 millième.
/!\ ATTENTION si CLAVIER, appuyer ensuite la touche ENTRÉE pour valider la modification.

- COULEURS un clic sur le bouton couleur modifie la couleur des prochaines branches.
On peut donc modifier la couleur de chaque niveau.

- Selon la valeur de k, on s'arrête à un certain niveau de profondeur de branches sous peine de ralentir la machine.

- RAZ réinitialise le tout.

PLEIN ECRAN

SOLUTION

Prenons comme unité la longueur de la branche de départ, dite à la profondeur (ou au niveau) zéro.
Chaque branche de profondeur immédiatement supérieure voit sa longueur multipliée par k.
Ainsi niveau 1 => longueur k ;
.

Et la branche de niveau n, a pour longueur k*..*k     n fois     SOIT     kⁿ.

Les branches ne doivent se recouper ni dans le sens de la hauteur ni dans le sens de la largeur.

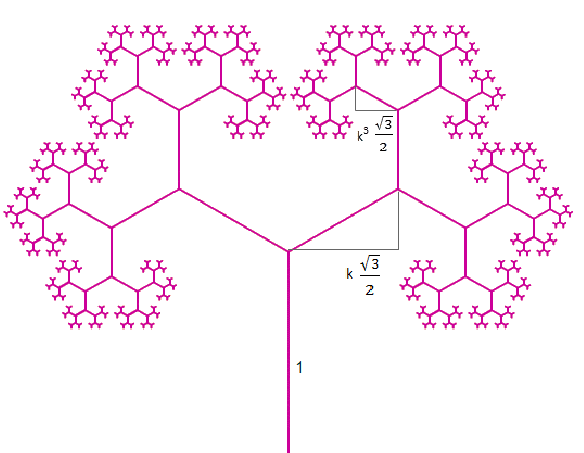
Dans le schéma ci-dessous, nous pouvons noter que les branches
    - sont verticales ou bien
    - font un angle de 30° en valeur absolue avec l'horizontale.
Analysons ces dernières par rapport à la largeur autorisée pour qu'elles ne se recoupent pas.
   La plus grande largeur disponible est .

Nous devons donc avoir :

La magie du nombre d'or...