|
Hyperboloïde de révolution réglé
Ellipsoïde de révolution avec des coupes elliptiques
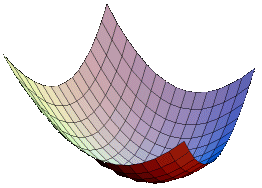
Paraboloïde avec coupes elliptiques
Un hyperboloïde réglé
L'hyperboloïde fait partie des quadriques, avec pour caractéristique principale de posséder un centre de symétrie et de s'étendre à l'infini.
L'hyperboloïde peut être obtenu comme intersection d'un cône de révolution et d'un plan...
Nous allons ici tendre des fils entre deux cercles de base.
L'enveloppe de ces fils tendus détermine un hyperboloïde centré sur le milieu du segment joignant les centres des deux cercles.
Observons le résultat selon l'angle (matérialisé par le segment témoin) que fait le segment joignant un cercle à l'autre.
ANIMATION
- Choisir de voir ou non le segment témoin.
- Choisir (avec les flèches) le nombre de segments qui seront tracés.
- Choisir de même le numéro du segment témoin.
- Choisir enfin la couleur des différents éléments :
.les cercles de base ;
.les fils et leurs noeuds ;
.le segment témoin.
- On peut STOPPER et RELANCER l'animation.
- La vitesse de l'animation est modulable à tout instant.
CLIQUER
Un ellipsoïde avec des coupes elliptiques
L'ellipsoïde fait partie des quadriques, avec pour caractéristique principale de ne pas posséder de point à l'infini.
Un ellipsoïde est un solide dont toutes les sections planes sont des ellipses.
Un ellipsoïde de révolution ou sphéroïde est une surface de révolution obtenue par rotation dans l'espace d'une ellipse autour de l'un de ses axes.
ANIMATION
- Choisir de voir ou non la coupe témoin.
- Choisir (avec les flèches) le nombre de coupes qui seront tracées.
- Choisir de même le numéro du témoin.
- Modifier les rapports définissant les coupes elliptiques du solide de révolution généré,
et observer.
- Choisir enfin la couleur des différents éléments :
.le tour elliptique ;
.les coupes ;
.la coupe témoin.
- On peut STOPPER et RELANCER l'animation.
- La vitesse de l'animation est modulable à tout instant.
Un paraboloïde à coupes elliptiques et autres...
Le paraboloïde fait partie des quadriques, avec pour caractéristique principale de ne pas posséder de centre de symétrie.
Certaines sections d'un paraboloïde avec un plan sont des paraboles.
Le paraboloïde de révolution est la surface obtenue en faisant tourner une parabole
autour de son axe.
On appelle paraboloïde elliptique de l'espace euclidien toute surface S pour laquelle il existe
un repère orthonormé (A,u,v,w) dans lequel S admet pour équation : x2/a2+y2/b2=2pz.
Un paraboloïde elliptique est donc une des cinq quadriques propres.
Un paraboloïde elliptique vérifie les propriétés suivantes :
l'intersection avec le plan y=0 est une parabole.
l'intersection avec un plan z=z0 est soit vide, soit une ellipse, soit un point.
si a=b, le paraboloïde est une surface de révolution.
ANIMATION
- Choisir de voir ou non la coupe témoin.
- Choisir (avec les flèches) le nombre de coupes qui seront tracées.
- Choisir de même le numéro du témoin.
- Modifier les rapports définissant les coupes elliptiques du solide de révolution généré,
et observer.
- Choisir enfin la couleur des différents éléments :
.le tour parabolique ;
.les coupes ;
.la coupe témoin.
- On peut STOPPER et RELANCER l'animation.
- La vitesse de l'animation est modulable à tout instant.
Comment obtenir un parabolïde elliptique avec une fonction z=f(x,y) .
C'est ICI
Comment obtenir un parabolïde hyperbolique avec une fonction z=f(x,y) .
C'est ICI