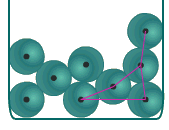
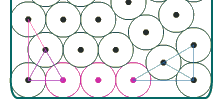
Quand
les bouteilles de champagne
s'alignent de façon magique dans le casier...
 Expérimentons Expérimentons
Choisir
avec le curseur la largeur du casier.
Choisir le
nombre de bouteilles, puis les placer dans la bouteille
-soit en cliquant dessus (elles entreront alors par la gauche)
-soit en les déplaçant avec la souris, elles se positionneront
naturellement.
Dans cette animation, les alignements seront automatiques à
partir d'une certaine ligne... à déterminer.
CLIQUER

 Quelques
résultats Quelques
résultats
Cette
fois, il n'y a aucune contrainte sur les espacements dans la ligne
du bas du casier.
L'alignement ne fonctionne pas toujours de façon systématique.
Chaque fois que l'espace entre deux boules est plus grand que le diamètre
multiplié par racine de 3, cela ne marche plus.
Essayer de comprendre pourquoi en observant les bouteilles... juste
observer attention ;o)
CLIQUER
Espacement entre les bouteilles
En observant
bien les résultats dans l'animation précédente
nous constatons qu'il existe des cas où l'alignement horizontal
des bouteilles n'a pas lieu.
Quand cela
a-t-il lieu ?
Soit d le diamètre de la bouteille, cela se produit quand la
distance entre les centres de deux bouteilles voisines dépasse
la valeur
d . .
Cette valeur est
la limite de la distance autorisée entre les deux centres pour
obtenir l'alignement magique.
Calage des
bouteilles sur les bords du casier
Nous verrons que si les bouteilles sont 'calées' contre les
bords du casier au moins tous les deux rangs en partant du bas, alors
nous obtenons un alignement magique à partir d'un certain rang.
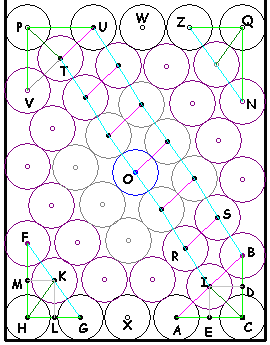
fig
C |
Ci-contre
(exemple obtenu avec la troisième animation
de cette page),
nous avons deux cas intermédiaires à gauche et
à droite.
Nous désignerons les bouteilles par leurs centres.
Cas où les bouteilles F, H,
G et B, C, A sont bien calées
dans le bas et sur les côtés du casier.
Les angles en H et en C sont droits.
.Démontrons
que les points B, I et A sont alignés
En H le raisonnement serait le même pour l'alignement
des points F, K et G.
Soit d le diamètre d'une bouteille :
d = BI.
De
même d = AI et d = CI car les bouteilles
se 'touchent' (elles sont tangentes).
(CI) est donc médiane dans le triangle rectangle
ACB.
Il s'ensuit que les points B, I et A sont alignés et
forment l'hypoténuse du triangle rectangle ABC.
Notons que [AB] est le diamètre du cercle
circonscrit au triangle ABC.
Nous avons montré que, lorsque
les bouteilles sont bien calées,
les
triangles verts en H et C sont rectangles
Remarquons que ce n'était pas le cas dans
la fig A.
|
.Démontrons
que l'on doit avoir AC < d  pour obtenir le calage de B sur le bord du casier
pour obtenir le calage de B sur le bord du casier
Supposons
AC = d  .
.
Soit E le milieu de [AC],
alors AC = d  / 2.
/ 2.
Avec D est le milieu de [BC], nous avons ID = EC et donc ID
= d  / 2.
/ 2.
Comme IB = d, nous déduisons de la relation ID = IB
 / 2 que le triangle isocèle BIC est équilatéral.
/ 2 que le triangle isocèle BIC est équilatéral.
Ceci signifie que BC = d c'est-à-dire que les deux cercles
de centre B et C sont tangents comme dans le cas de la fig B
précédente.
Si donc AC > d  alors la bouteille de centre B ne sera plus calée sur le bord
du casier. C'est le cas à droite de la fig A.
alors la bouteille de centre B ne sera plus calée sur le bord
du casier. C'est le cas à droite de la fig A.
.Démontrons que les angles en
P et Q sont droits
Tous
les segments dessinés en rose, ont une longueur égale
au diamètre d des bouteilles.
Il en est de même de chacun des segments de couleur bleu ciel.
Le quadrilatère RSBI a 4 côtés de même
longueur. C'est un losange et ses côtés opposés
sont parallèles.
Nous avons (RS) // (IB) et RS = IB.
En étudiant, de proche en proche, chacun des losanges dessinés
en rose et bleu ciel, nous démontrons que TU = IB et
(IB) // (TU).
De la même façon, nous arriverions à AI = VT
et (AI) // (VT).
Comme (AI) // (IB), nous déduisons que (VT) // (TU),
c'est-à-dire que les points V, T et U sont
alignés.
Comme AI = IB, nous déduisons que VT = TU.
VT = TU et (VT) // (TU) impliquent que les points V, T
et U sont alignés.
Par ailleurs PT = TU = VT.
Le triangle UPV est ainsi inscriptible dans le cercle de diamètre
UV de rayon d, de centre T.
Il est donc rectangle.
Comme VP
est vertical (V appuyé sur le bord du casier),
nous en déduisons que (PU) est
horizontal.
De même on montrerait que (QZ)
est horizontal.
Remarque
:
Les triangles
UPV et ACB ont leurs côtés parallèles
et ils ont même hypoténuse. Ils sont donc superposables.
Il en est de même pour les deux triangles GHF et ZQN.
.Démontrons
que les points U, W et Z sont alignés sur une droite horizontale

fig
D |
Le point O est parfaitement déterminé
à partir des bouteilles colorées en rose, bleu
et vert à un niveau inférieur au sien.
Les bouteilles colorées en noir stabilisent l'ensemble
par l'appui sur les bords du casier
Nous avons vu que les triangles du bas gauche et droite se retrouvaient
symétriquement en haut du casier.
Les positions des bouteilles intermédiaires se retrouvent
aussi symétriquement (par construction)
dans la partie supérieure du casier.
O est centre de symétrie de la figure
complète.
Ainsi W est l'image de X dans cette
symétrie centrale.
De même U est symétrique de A
et Z est symétrique de G.
Il
s'ensuit que la droite horizontale (GXA) a pour
image (UWZ)
qui est aussi une droite horizontale.
|
P,
U, W, Z et Q (notations
fig C) sont finalement tous
alignés horizontalement.
Les bouteilles sont alignées horizontalement sur la ligne du
haut du casier dans la fig D.
Ce raisonnement
reste valable, quel que soit le nombre de bouteilles en bas du casier,
pourvu que les bouteilles soient bien calées et donc que les
intervalles entre les boules voisines soient inférieurs à
d  . .
S'il y a n bouteilles
touchant le bas du casier, le point O se trouve sur sur la n ème
oblique.
De façon générale, l'alignement magique se produira
sur la 2n-1 ème rangée horizontale.

 Vérifications Vérifications
Soit
d le diamètre d'une bouteille et n le nombre de
bouteilles dans le bas du casier.
La largeur du casier
est égale à d ( n - 1 + )
si les espaces sont contrôlés, )
si les espaces sont contrôlés,
sinon elle est un peu
plus grande mais légèrement inférieure à
d ( n + 1) .
Dans
ce dernier cas, l'espace entre deux bouteilles peut être plus
grand que d
et l'alignement n'est pas
systématique.
ANIMATION
.Choisir
le nombre de bouteilles dans le bas du casier
.Indiquer
si les espaces sont contrôlés ou non.
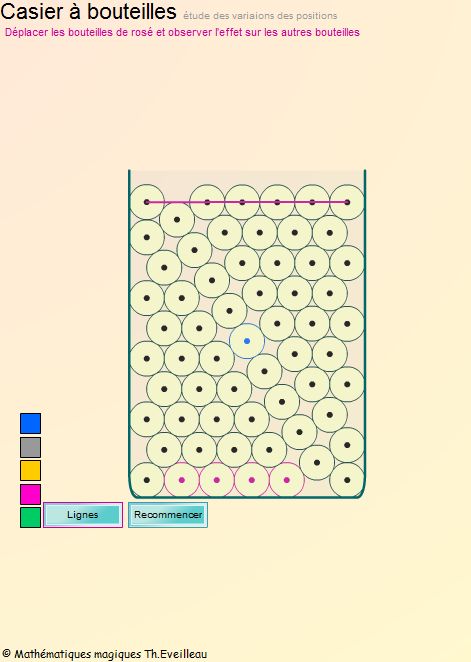
.Déplacer
les bouteilles de rosé dont
le centre est un gros point rouge
en bas du casier.
Il suffit de déplacer ces points avec la souris.
Observer
l'effet sur les autres bouteilles.
.Cliquer
deux par deux les autres bouteilles pour tracer les segments de droite
qui joignent leurs centres.
.Les
bouteilles roses peuvent être à la fois déplacées
et utilisées pour tracer des segments de droite.
Pour cela
-après
avoir cliqué sur
le bouton Lignes, on peut tracer des segments de droite
entre les différentes bouteilles y compris les roses ;
-après avoir cliqué sur bouton Déplacer
on peut déplacer à nouveau ces bouteilles roses.
A tout instant on peut modifier la couleur
des tracés des segments de droite en cliquant sur la couleur
désirée.
On pourra observer, l'effet sur les longueurs et alignements des segments
de droites.
CLIQUER
Cette situation est également
présentée dans le problème N°44 de "
Which way did the bicycle go? "
C'est aussi le problème N°D442
2 de www.diophante.fr

|