Le problème Résultat Manipulations et explications  Pourquoi les bulles de savon sont-elles sphériques ?  Cliquer

Le problème

Un disque métallique auquel on a attaché une petite ficelle, avec un nœud ouvert. On plonge ce disque dans un liquide savonneux : par exemple du liquide vaisselle auquel on a ajouté éventuellement un peu de glycérine. Nous allons piquer l'intérieur savonneux de la ficelle avec un crayon. Que va-t-il se passer ? Quel est donc le rapport avec les mathématiques ?

Résultat

MAGIQUE ! La ficelle prend instantanément la forme d'un cercle évidé parfait. L'eau savonneuse forme maintenant une couronne entre deux cercles. Elle occupe une surface minimale. Pour cela la partie évidée occupe au contraire une surface maximale : celle d'un disque. Nous allons voir ci-dessous qu'à périmètre constant, la forme dont l'aire est maximale est le disque. Ce problème appelé problème isopérimétrique, correspond à celui issu du mythe de la reine Didon lors de la création de Carthage au 9è siècle avant Jésus-Christ : trouver la forme géométrique qui maximise son aire avec un périmètre fixé.

La légende, selon le poète Virgile, raconte que la reine Didon dut s'enfuir après que son frère eut assassiné son époux.
Elle demanda asile aux autochtones de Byrsa ("la peau de bœuf") près de Tunis.
On ne lui concéda que ce qu'une peau de bœuf pourrait couvrir.
Aussi en femme avisée et mathématicienne avant l'heure, elle la découpa en fines lamelles,
de façon à obtenir une longueur de plus de 2000m (d'aucuns disent 4000m...).
Elle disposa cette corde en un demi-cercle dont le diamètre était la côte de Byrsa (quasi rectiligne).
C'est ainsi qu'elle trouva parmi toutes les courbes fermées, celle qui délimite la plus grande surface possible : un cercle.
Ce résultat est aussi appelé : "théorème de Didon ".
Il a fallu de nombreuses années aux mathématiciens pour démontrer ce théorème.
Nous allons expérimenter quelques étapes de la démonstration.

Manipulations, explications

.Dans l'exemple suivant, le triangle a un périmètre constant

Essayer de trouver la forme donnant l'aire MAXIMALE.

-Choisir d'emblée le périmètre avec le bouton adéquat.
-Déplacer les ponts A, B ou C avec la souris ou le clavier.
-Quand le triangle est bon, un petit bip et un message le signalent.

Reprendre ensuite les déplacements avec la souris pour continuer.

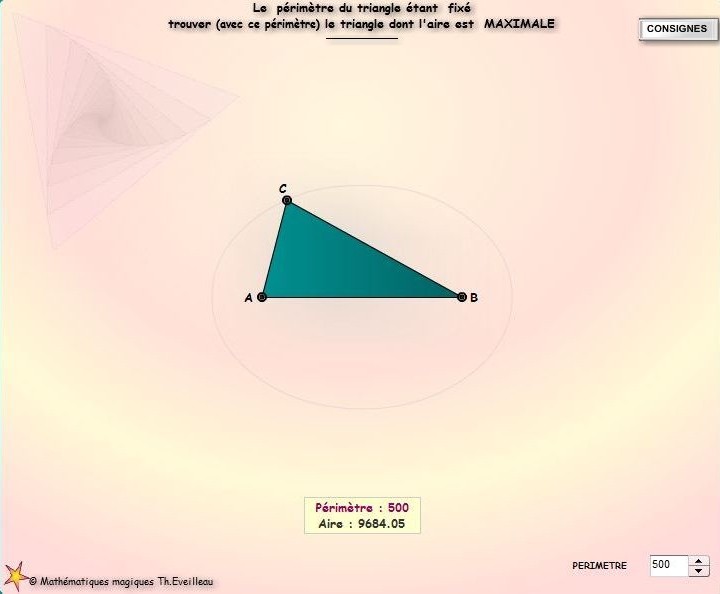
Résultat

Le triangle a une aire maximale quand il est régulier.
C'est à dire quand il est équilatéral : trois côtés de même mesure et trois angles égaux de 60°.
Parmi tous les triangles ayant un périmètre donné p, le triangle équilatéral est celui de plus grande aire.

Pour trouver plus facilement le bon triangle dans l'animation précédente, essayer d'anticiper l'aire cherchée.
C'est celle du triangle équilatéral dont le côté mesure un tiers du périmètre donné.

Et l'aire d'un triangle équilatéral de côté a est : a²/4.

.Observons maintenant un rectangle ayant un périmètre constant

Essayer de trouver la forme donnant l'aire MAXIMALE.

- On peut stopper l'animation avec le bouton STOP et la remlancer avec le bouton ANIMER.
- Déplacer le point Largeur avec la SOURIS ou le CLAVIER avec les flèches Gauche ou Droite quand l'animation est stoppée.
- Quand l'aire est maximale, un petit bip et un message le signalent.

Dans l'exemple suivant, le préimètre du rectangle est fixé à 12 unités.

CLIQUER

Résultat

Le rectangle a une aire maximale quand il devient régulier.
C'est à dire quand il devient carré : quatre côtés de même mesure.
Parmi tous les rectangles ayant un périmètre donné p, le carré est celui de plus grande aire.

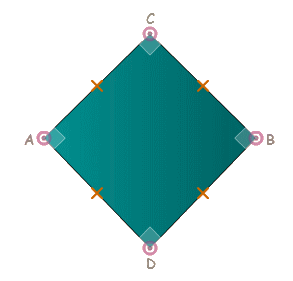
.Cette fois, il s'agit d'un quadrilatère quelconque ayant un périmètre constant


Essayer de trouver la forme donnant l'aire MAXIMALE.

- Choisir d'emblée la longueur des deux côtés supérieurs puis inférieurs en déplaçant le point P sur le segment.
  La longueur totale de ce segment représente le périmètre imposé de la figure.
- Déplacer ensuite chacun des quatre points à volonté pour modifier l'aire de la figure.

- Au CLAVIER, les flèches Gauche ou Droite permettent de déplacer le dernier point cliqué.
- Quand l'aire est maximale, un petit bip et un message le signalent.

CLIQUER

Résultat

Là aussi le quadrilatère a une aire maximale quand il est régulier :
quatre côtés de même mesure et quatre angles de 90°.
C'est un carré, chaque côté mesure 200 pixels et la surface mesure 40 000 pixels carrés.

Parmi tous les quadrilatères ayant un périmètre donné p, le carré est celui de plus grande aire.

Voici la solution pour l'animation précédente.
Notos que le succès ne peut être obtenu qu'après avoir placé le point P au milieu du segment correspondant au périmètre de la figure.

Les résultats pour un polygone ayant trois côtés, puis quatre côtés se généralisent à un nombre quelconque de côtés.

Parmi tous les polygones ayant n côtés et de même périmètre p, le polygone régulier est celui qui a la plus grande aire.

Remarque
un polygone régulier a tous ses côtés de même mesure ET tous ses angles de même mesure.

L'étape suivante consiste à montrer que :
de tous les polygones réguliers et à même périmètre, c'est celui qui a le plus de côtés qui couvre la plus grande surface.
Le cercle, "polygone régulier" à nombre infini de côtés, est donc celui dont l'aire est la plus grande.

Revenons au disque et la ficelle dans l'eau savonneuse

Le mince film d'eau savonneuse tend à utiliser une surface d'aire minimale (principe de minimisation).
Ainsi pour que la couronne ait une aire minimale, la partie évidée dans la ficelle doit avoir une aire maximale enfermée dans le périmètre fixe de la ficelle.
La forme obtenue est donc un cercle.

Oh... quelle belle nature mathématicienne !

Bulles sphériques

Les bulles de savon amusent les enfants et tout autant les adultes ! Chacun a pu constater que lorsqu'il n'y a ni vent ni courant d'air, les bulles ont la forme de sphères. Une bulle de savon est un globe formé d'un mince film d'eau savonneuse rempli d'air qui flotte dans l'atmosphère. Une bulle de savon tend donc, naturellement, à prendre la forme qui lui permet d'enfermer un volume d'air donné dans une surface d'aire minimale ; il s'agit d'une sphère. La démonstration n'est pas si facile et Archimède en tête, a travaillé ce problème

En 1882, le mathématicien allemand Hermann Amandus Schwarz prouve que :
parmi toutes les surfaces enfermant un volume donné, la sphère est bien celle qui présente l'aire minimale.

Mathématiquement, la sphère donne le plus petit rapport surface / volume.
Si R est le rayon de la bulle,
.la surface est : S = 4πR²
.le volume est : V = 4πR³ / 3
et
enfin le rapport est : S / V = 3 / R .

Physiquement, les molécules ont tendance à se tenir rapprochées les unes des autres, comme si elles étaient reliées par de petits ressorts.
Comme il n'y a pas d'attraction privilégiant une direction plutôt qu'une autre sur une bulle, la forme la plus stable est une sphère.

Pour aller plus loin et réaliser de jolies bulles :
http://fr.wikipedia.org/wiki/Bulle_de_savon
http://scienceamusante.net/wiki/index.php?title=Bulles_de_savon_g%C3%A9antes