|  Problème
Mais pourquoi donc nos ustensiles
sont-ils si souvent fabriqués selon les mêmes
proportions, quelles que soient leurs dimensions ?
Et pourquoi la hauteur d'une casserole est-elle approximativement
égale à son rayon quelle que soit sa contenance
? |
 Histoire...
La
petite fée du logis ... voulait offrir à
son prince une quantité fixe d'une potion dans un
chaudron en or de sa fabrication. Bien sûr elle devait
utiliser le moins d'or possible pour ce
chaudron en forme de cylindre qui avait une contenance
et une épaisseur fixes.
Il
fallait donc que la surface totale du chaudron soit minimale.
Et
comme elle était futée elle trouva que le rayon
du fond du chaudron devait être
égal à la hauteur de
celui-ci pour utiliser le moins d'or possible ! |
|
C'est ainsi
que depuis ce temps-là, nos casseroles ont toutes
une hauteur approximativement égale au rayon de leur fond...
Explication
graphique et dynamique
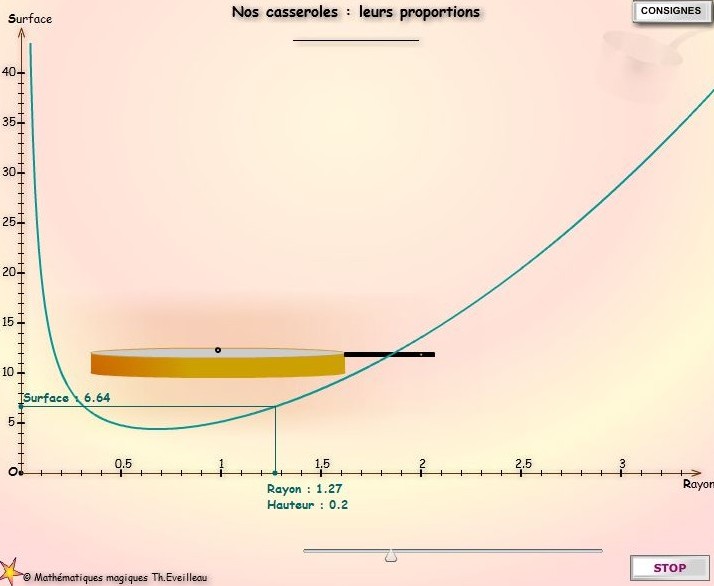
Prenons,
par exemple, une capacité fixe de 1 unité arbitraire
La quantité
de matière est minimale en même temps que la surface S
de la casserole pour une épaisseur donnée.
Dans
l'animation suivante, le volume de la casserole est fixé : c'est
une unité.
Lorsque la solution donnant
une surface minimale est rencontrée, une pause de deux secondes
a lieu et un petit bip sonore se fait entendre.
-On peut stopper l'animation automatique en cliquant le bouton STOP,
on la relance en cliquant le bouton ANIMER.
-On peut faire varier le rayon manuellement avec la SOURIS ou au CLAVIER
avec les flèches GAUCHE et DROITE.
On observe que la surface
est minimale quand le rayon est égal à la hauteur.
Sur la courbe la précision est au pixel près, modifiez
donc doucement le rayon pour voir apparaître le MINIMUM
de la surface.
En
savoir un peu plus
Pour
une hauteur h, un rayon R et un volume donnés, on a la relation
:
V
= π R² h donc
h = V / π R² et la surface
S = π R²+
2 π R h
soit π R² + ( 2 π R ) (V /
π R²)
Choisissons
un volume unité : V=1,
S
= π R² + 2 / R et h
= 1 / ( π R²) (**)
Quand
on observe l'animation donnant l'évolution de la surface du
matériau de la casserole en fonction de R,
on note que cette surface est minimale
quand h=R.
En effet,
La fonction S(R) a
pour dérivée 2 π R - 2 / R².
Cette dérivée s'annule pour un minimum de la surface
en un rayon, tel que R3 = 1/π.
Dans ce cas nous avons π = 1/R3 ET avec la relation
(**) :
h = R3/R² = R.
h=R.
CQFD
|
