Cryptographie Son une édtue de l'Uvinertisé de Cmabrigde, l'odrre des ltteers dnas un mtos n'a pas d'ipmrotncae, la suele coshe ipmrotnate est que la pmeirère et la drenèire soit à la bnnoe pclae.Le rsete peut êrte dnas un dsérorde ttoal et vuos puoevz tujoruos lrie snas porlblème. C'est prace que le creaveu hmauin ne lit pas chuaqe ltetre elle-mmêe, mias le mot cmome un tuot.

La substitution et l'analyse de fréquences

La méthode choisie dans l'animation présentée ci-après est celle de la substitution. Chaque lettre est remplacée au hasard par une autre lettre.

Dans la méthode de chiffrement par substitution, une lettre du message original "garde sa position mais change de rôle". Le fait de "garder sa position" rend possible la cryptanalyse par l'étude des fréquences.
Nous devons cette méthode à l'ingéniosité d'al-Kindi qui du coup a inversé le rapport des forces entre les cryptographes et les cryptanalystes.

Al-Kindi est né à Bagdad en l'an 801. Il fut médecin mathématicien et linguiste. On ne connaît son rôle de pionnier en cryptanalyse que depuis 1987. Dans les archives à Istanbul, on découvrit alors une copie de son traité 'Manuscrit sur le déchiffrement des messages cryptographiques'.

A partir d'un texte suffisamment long, il propose de classer les lettres selon leur fréquence d'apparition. On fait ensuite la même chose avec le texte à déchiffrer :
"En classant les symboles par ordre décroissant de leur fréquence d'occurrence, on les remplace par les lettres correspondantes, jusqu'à épuiser tous les symboles du cryptogramme à décrypter".

Ainsi dans cette méthode, il suffit de comptabiliser les occurrences de chaque caractère chiffré et de les comparer le tableau des fréquences de la langue dans laquelle il a été écrit.
Bien sûr, cette méthode ne fournit pas toujours la solution directement. Si le texte est court, c'est plus délicat : ainsi le 'E' ne sera peut-être pas le caractère le plus fréquent.
Regarder alors le 'S', le 'A' le 'I' ou le 'N'...
Repérer les lettres doubles ('L', ou 'N' ), les associations de lettres 'OU', 'IN', 'QU' etc.

En repérant les fréquences, groupes de lettres et autres on peut réussir le décryptage d'un texte même assez court.

ANIMATION

Ci-dessous, essayer de décrypter l'un des cinq textes proposés (cliquer sur le bouton choix du texte).

Il est possible d'entrer son propre texte à la place de celui qui est proposé ; cliquez ensuite sur codage pour le crypter et faites-le décoder par un ami.
La fréquence des lettres dans le texte chiffré est mise à jour à chaque transformation.
Le tableau donnant la fréquence des lettres dans un texte habituel en français aide à décoder le texte donné : ces résultats sont obtenus à partir de divers textes récents écrits en langue française dans lesquels on a tiré au hasard une lettre
(Source : Histoire des codes secrets » de Simon Singh (Edition J.C. Lattès, 1999).

CLIQUER

 

 

Exemple avec Sherlock Holmes

Dans Les Hommes dansants, Conan Doyle mit Sherlock Holmes face au décryptage d'un message chiffré par substitution. Pour le déchiffrer le détective doit utiliser l'analyse des fréquences dans la langue anglaise.

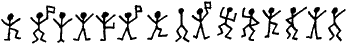
Solution
AM HERE ABE SLANEY

Remarques
Pour transmettre un message, Jules César rasait la tête d'un esclave, inscrivait le message sur son crâne, attendait la repousse des cheveux et envoyait l'esclave... Procédé long et fastidieux !
Pour transmettre des ordres ou des rapports à ses lieutenants, il ne faisait pas confiance aux messagers et codait ses messages : chaque lettre était remplacée par une autre obtenue avec un décalage de l'alphabet.
Ce code de César est la méthode de cryptographie la plus ancienne communément connue dans l'histoire.

En cryptographie, le texte original est appelé texte clair ou libellé. Le texte camouflé est appelé texte chiffré ou cryptogramme.
Le chiffrement est le procédé qui permet de convertir un texte clair en cryptogramme. Le déchiffrement est l'inverse.

De nombreux systèmes cryptographiques ont été inventés au cours des siècles.

La plupart des méthodes de chiffrement reposent sur deux principes essentiels : la substitution et la transposition.

La substitution consiste à remplacer certaines lettres par d'autres ou par des symboles. Les disques d'Alberti : Il s'agit d'un chiffreur portatif comportant un disque fixe sur lequel est chiffré un alphabet et un disque mobile où est gravé un autre alphabet. L'émetteur en faisant tourner le disque mobile apparie un alphabet à un autre alphabet qui deviendra l'alphabet chiffré. Ici D devient M, I devient R... Pour décrypter le message le récepteur a seulement besoin de positionner le disque central dans la même position que celle de l'émetteur. La connaissance de la correspondance de deux lettres est suffisante. On peut utiliser plusieurs anneaux mobiles rendant le décryptage plus difficile : chiffrage polyalphabétique (Vigenère). Dans ce cas, le chiffre résiste bien à l'analyse de fréquences. Ce dispositif était utilisé lors de la guerre de Sécession nord-américaine.

La transposition signifie que les lettres du message sont permutées afin de rendre le texte incompréhensible.

Enigma
En 1923, l'ingénieur allemand Arthur Scherbius breveta la machine Enigma (devenue synonyme de secret militaire). Le décryptage d'Enigma par les gouvernements qui affrontèrent l'Allemagne nazie, a été essentiel pour la résolution du conflit par les alliés. C'est une histoire fascinante faisant essentiellement intervenir les services de renseignements de Pologne et du Royaume-Uni. L'un de ses héros fut Alan Turing considéré comme le père de l'informatique moderne.

Depuis la Seconde Guerre Mondiale, la cryptographie a fait d'énormes progrès et la sécurité des systèmes est devenue également bien supérieure.

L'algorithme RSA (sigle des noms de famille Rivest, Shamir et Adelman), est assidûment employé aujourd'hui.
Cet algorithme a été présenté en 1977 par Gardner, divulgateur scientifique de renom. Il s'agit d'un système à clé publique. Le défi de Gardner consistait à décomposer le nombre suivant
N = 114 381 625 757 888 867 669 235 779 976 146 612 010 218 296 721 242 362 562 561 842 935 706 935 245 733 897 830 597 123 563 958 705 058 989 075 147 599 290 026 879 543 541
en produit de deux facteurs premiers : N = p q.
La réponse devait être envoyée à ses créateurs Rivest, Shamir et Adelman au Laboratoire d'informatique du MIT.

Il fallut 17 ans pour que la collaboration de plus de 600 personnes permette de trouver le résultat.

L'algorithme RSA utilise les propriétés des nombres premiers.
Cet algorithme est fiable parce qu'il repose sur la décomposition de très grands nombres en facteurs premiers. Actuellement les nombres employés pour le chiffrement des messages les plus confidentiels utilisent plus de 200 chiffres. Et aucun ordinateur ne permet de déterminer les deux facteurs premiers p et q en un temps raisonnable.

Les applications civiles sont très nombreuses : banques, télécommunications, cartes bleues...

A l'ère du traitement quantique, nouvelle forme révolutionnaire d'utiliser les ordinateurs, encore théorique, la puissance des machines sera tellement grande qu'il faudra revoir tout le système de cryptographie actuel. La recherche d'un cryptosystème quantique élaboré est déjà en route.

 

Pour en savoir plus http://www.bibmath.net/crypto/index.php3
et
Le monde est MATHEMATIQUE
CODAGE ET CRYPTOGRAPHIE
Mathématiciens, espions et pirates informatiques
collection présentée par Cédric Villani