Comment trouver le coffre de plus grande valeur ?

Le problème, c'est le n° G141 de Diophante :

Puce a écrit 8 entiers distincts sur 8 cartes qu’il met dans un chapeau. Le plus grand de ces entiers est N. Zig qui n’a aucune idée de l’amplitude de l’intervalle à l’intérieur duquel se situent les entiers, a pour objectif de trouver N. Pour ce faire, il a le droit de tirer les cartes du chapeau une par une. Il doit déclarer la valeur de N immédiatement après avoir tiré une carte sans pouvoir déclarer l’un quelconque des nombres obtenus lors des tirages antérieurs. Montrer qu’il dispose d’une méthode qui lui permet d’annoncer la valeur de N avec plus de 40 chances sur 100.
Généralisation avec 2016 entiers . Montrer que la probabilité de succès de Zig est supérieure à 35 chances sur 100.

ANALYSE

Je vais utiliser des coffres contenant des trésors d'une valeur aléatoire.
Les valeurs des coffres sont toutes différentes.
Nous voulons choisir le coffre ayant la plus grande valeur.

La bonne stratégie consiste à laisser défiler un certain nombre de coffres. Bien observer et mémoriser leur valeur.
Attendre ensuite qu'un coffre de valeur supérieure à chacun de ces k premiers coffres se présente.
Choisir et garder ce dernier coffre.

Comment choisir le nombre de coffres ? Là est la question.

Les trois animations suivantes vont vous aider à réfléchir et imaginer la bonne réponse.
-La première permet de comprendre et d'expérimenter pas à pas.
-La deuxième est plus rapide et permet de répéter rapidement un grand nombre d'expériences tout en faisant varier les variables n et k : n nombre total de coffres et k : valeur du point d'arrêt optimal.
-La troisième permet des tests sur un très grand nombre d'expériences et donc aide à déterminer rapidement la meilleure valeur de k en fonction de n.

 

Animations pour comprendre, expérimenter et conjecturer

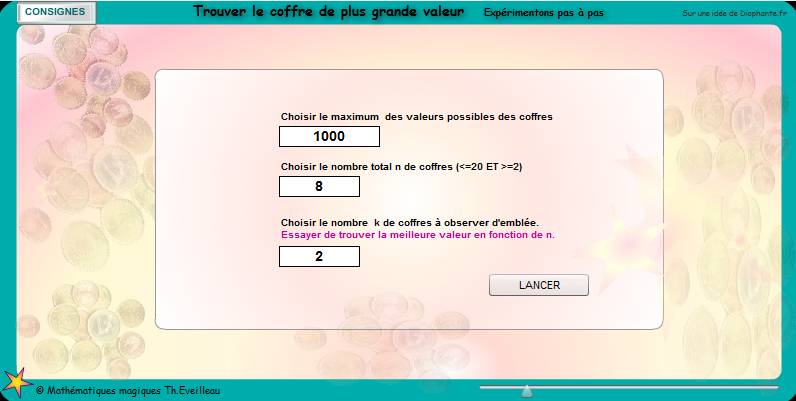
.Comprendre la procédure utilisée en expérimentant pas à pas

-Choisir le nombre n maximum de coffres.
-Choisir le nombre k de coffres qui vont défiler.
Ensuite on choisit le premier coffre de valeur supérieure aux k premiers.

--> Le pourcentage de réussite est affiché.
Si le coffre sélectionné est le meilleur des n coffres alors c'est gagné le taux de réussite est incrémenté, sinon il vdiminue.

A vous de faire varier k en fonction de n et d'essayer de trouver la meilleure valeur.

Notons que le choix de la valeur maximale des coffres ne change rien au résultat, inutile de prendre des valeurs trop grandes, cela permet juste d'effectuer un tirage aléatoire de la valeur des coffres.
Cette valeur doit bien entendu être supérieure au nombre de coffres qui ont tous des valeurs différentes.

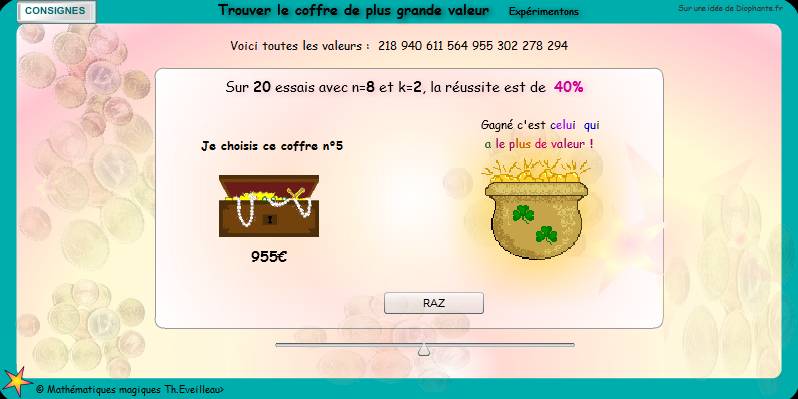
.Expérimenter rapidement et observer les pourcentages obtenus

Même démarche entrer les valeurs de n et de k.
Faire varier n en fonction de k et relancer le processus.
Analyser alors les résultats sur un grand nombre d'expériences.

CLIQUER

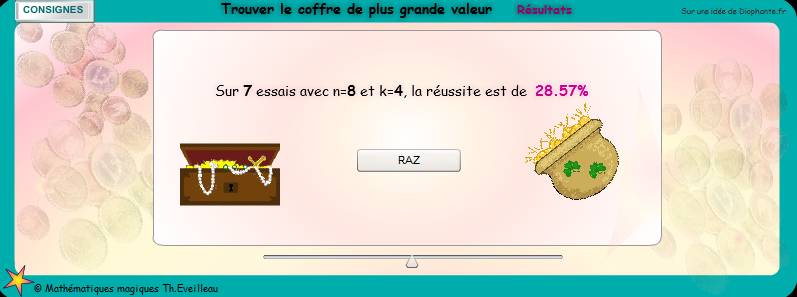
.Expérimenter encore plus rapidement

Même démarche entrer les valeurs de n et de k.
Faire varier n en fonction de k et relancer le processus.
Analyser alors les résultats sur un très grand nombre d'expériences.

CLIQUER

Résultats

Pour obtenir les meilleurs pourcentages de réussite, la bonne stratégie est de laisser passer environ k = 37% des n coffres (précisément 1/e ~ 36,787944 ) quand n est grand).
Ensuite attendre un coffre de valeur plus grande valeur, que celle des coffres de ce premier échantillon de k coffres.
On parle de règle des 37%.

Avec cette procédure, on peut obtenir 40% de chances de réussite avec n=8 coffres et plus de 35% pour n=2016.

Ainsi avec n = 8 coffres en tout, laisser passer k = 3 coffres et choisir ensuite le premier coffre de plus grande valeur que les 3 premiers.
Avec n = 10 coffres en tout, laisser passer k = 4 coffres et choisir ensuite le premier coffre de plus grande valeur que les 4 premiers.
Avec n = 40 coffres en tout, laisser passer k = 15 coffres et choisir ensuite le premier coffre de plus grande valeur que les 16 premiers.
Avec n = 1000 coffres en tout, laisser passer k = 369 coffres et choisir ensuite le premier coffre de plus grande valeur que les 369 premiers.

Ce sont des résultats probabilistes. Il ya aura donc quelques variantes dans les meilleurs résultats.

N'hésitez pas à les tester avec la troisième animation ci-dessus.

En savoir plus,
démonstrations mathématiques :

Avec Diophante
:http://www.diophante.fr/problemes-par-themes/g-probabilites/g1-calcul-des-probabilites/3689-g141-le-choix-du-bon-numero.


Ce problème est connu sous différentes appellations, voici (liens externes) quelques exemples expliqués commentés


-The marriage problem ou the Secretary problem (Thomas Ferguson 1989).

-Une très bonne analyse ici avec les filles du sultan à marier : the sultans Dowry P roblem.
          http://mathworld.wolfram.com/SultansDowryProblem.html.

-Le problème de la décision avec quelques exemples expliqués clairement et simplement.

On trouve également dans cette page une critique assez sympathique quant aux choix pris sur un critère purement mathématique dans la vie courante.

- http://www.math.uah.edu/stat/urn/Secretary.html

-Savoir quand s'arrêter.


Autres résultats

Quelques résultats avec : résultats avec the secretary problem or the marriage problem.