Le problème

Marie et Julie vont régulièrement chez leur coiffeur BoucleTifs.
Elles y vont chaque samedi, leur jour de congé, pendant une heure et quart.
BoucleTifs peut les recevoir de dix heures à dix-sept heures.
Souci :
Julie est l'ex femme de Martin et Marie son épouse actuelle.
Elles aimeraient bien ne pas s'y rencontrer.

Elles s'y rendent donc à des horaires tout à fait aléatoires.

Pourtant Marie et Julie s'y retrouvent bien plus souvent qu'elles ne le désirent.

Pouvez-vous dire en moyenne à quelle fréquence elles s'y rencontrent ?

ANIMATION

- Choisir entre :
     JOUER mode pas à pas pour une observation de chaque étape ou
     SIMULATION avec de multiples expériences consécutives.

En mode JOUER, cliquer sur le bouton fléché pour réaliser une nouvelle expérience ;
En mode SIMULATION, cliquer sur le bouton GO pour lancer les expérimentations ;
     - SI le bouton Ultra rapide est coché, le résultat est immédiat ;
     - SINON chaque rendez-vous est représenté par le couple (x ,y) des heures d'arrivée de Marie. et Julie.
     En rouge, (Julie première arrivée), en vert (Marie première arrivée) -> il n'y a pas de rencontre.
     En noir il y a rencontre.

SOLUTION

Pour analyser la situation désignons par
    x, l'heure de départ de Marie et par
    y l'heure de départ de Julie.

 x et y ont pour unité l'heure.

La séance chez le coiffeur dure une heure et quart, c'est-à-dire 1,25h.

Pour que ces deux dames ne se rencontrent pas, il faut
- soit que Julie arrive plus d'une heure et quart avant Marie , donc que : y < x-1.25        (*)
- soit que Julie arrive plus d'une heure et quart après Marie , donc que : y > x+1.25       (**)

L'équation limite de (*) est représentée par y = x - 1.25 est représentée dans les limites horaires imposées par la ligne oblique rouge ci-dessous.
Les couples satisfaisant la relation sont donc tous les couples (x,y) situés à l'intérieur du triangle rouge, frontière oblique d'ailleurs exclue.

De même l'équation limite de (**) est représentée par y = x + 1.25 est représentée dans les limites horaires imposées par la ligne oblique verte ci-dessous.
Les couples satisfaisant la relation sont donc tous les couples (x, y) situés à l'intérieur du triangle vert, frontière oblique d'ailleurs exclue.

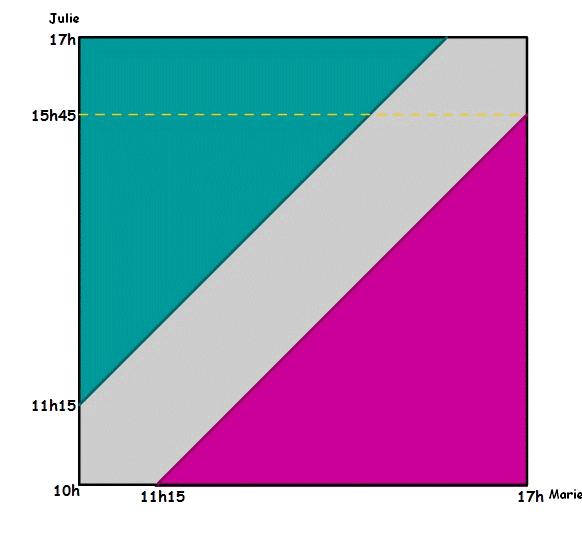
Ainsi Julie et Marie se rencontreront si leurs heures d'arrivée x et y correspondent aux couples e la zone coloriée en gris ci-dessous.

L'aire d'une ligne étant nulle on ne tient pas compte de la frontière.

L'aire totale du carré complet est 7 * 7 = 49
L'aire de la parie gris et rouge réunies, est celle d'un carré de côté 7-1.25 = 5.75.
C'est donc 5.75 * 5.75 = 33.0625

L'ai de la partie grise est : 7*7 -5.57*5.75 = 49 - 33.0625 SOIT 15.9375

La probabilité cherchée est le rapport de l'aire grise sur l'aire totale SOIT 15.9375/48 ~ 0.325255...

C'est environ 32.5 %

Cela signifie que Julie et Marie se rencontrent quasiment une fois sur trois.


 

L'animation précédente confirme ce résultat dès que l'on effectue un assez grand nombre d'expériences.

---