Le crible géométrique Comment et pourquoi ça marche

---

  

Le crible géométrique

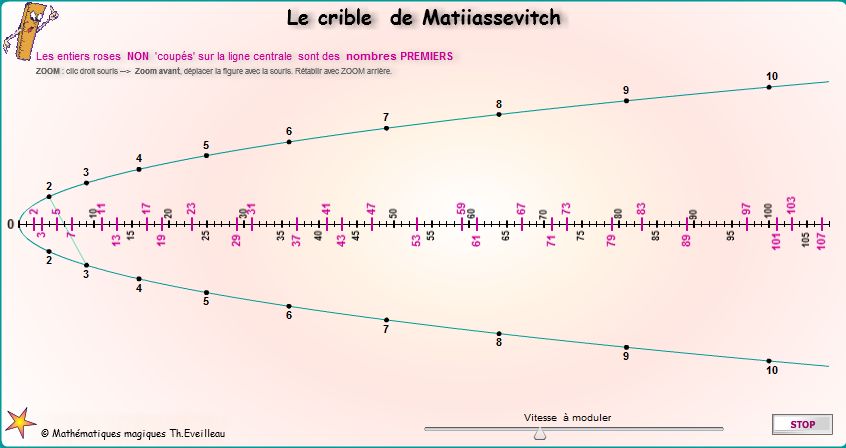
Ci-dessous une parabole et son axe de symétrie horizontal.
Le produit de deux nombres entiers notés sur chaque branche de la courbe, se lit directement à l'intersection du segment vert et de l'axe de la parabole (la ligne droite médiane qui est l'axe de symétrie de la parabole).

En plaçant des points de coordonnées entières sur chaque branche de la parabole et en les reliant systématiquement par des segments coupant l'axe de symétrie, on obtient les produits de ces deux entiers.
Les points (à abscisse entière) de l'axe par lesquels les segments ne passent pas sont donc des nombres premiers (2).

Ainsi nous obtenons un crible géométrique très simple pour trouver les nombres premiers.
Cette idée simple et géniale nous vient des mathématiciens russes Yuri Matiiassevitch et Boris Stechkin. 

Dans l'animation ci-dessous, ne pas hésiter à
- moduler la vitesse ;
- stopper ou relancer l'animation ;
- zoomer avec le clic droit de la souris (après avoir cliqué à l'intérieur de l'animation).

Cliquer ici pour la table de multiplication correspondante animée.
Cliquer ici pour l'image du crible.

Comment et pourquoi ça marche 

La clé réside dans la parabole.
En replaçant à l'horizontale les abscisses et l'axe des abscisses nous comprendrons mieux.
La parabole a pour équation y=x².
Considérons m et n positifs.
Le point M a pour abscisse m et le point N a pour abscisse -n.

Cherchons l'équation de la droite (MN).
Elle passe par les points de coordonnées (m,m²) et (-n,n²).
L'équation de cette droite est donc :

y -m² = [(m² - n²) / (m - (-n))] (x - m)
y -m² = [(m + n)(m - n) / (m + n)] (x - m)
Soit
y - m² = (m - n) (x - m)
ou
y = (m - n )x - m² + mn + m²
soit
y = (m - n )x + mn

Quand x = 0, y = mn

Finalement la droite (MN) coupe l'axe des y, au point d'ordonnée mn, qui correspond bien au produit cherché. 

  Voir aussi la table de Matiiassevitch.

   

(1) Source : Merveilleux nombres premiers de Jean-Paul Delahaye BELIN. Pour la science 

(2) Un nombre est dit premier, s'il admet exactement 2 diviseurs distincts (lui-même et l'unité). 1 n'est donc pas premier.