Problème

Nous devons traverser l'étendue d'eau qui entoure l'île. Mais celle-ci est infestée de voraces alligators. Nous disposons de quatre barres étroites qui ne flottent pas. Chacune mesure exactement 9,5 m. Comment procéder ?

 

 

 

 

 

 

CHERCHONS

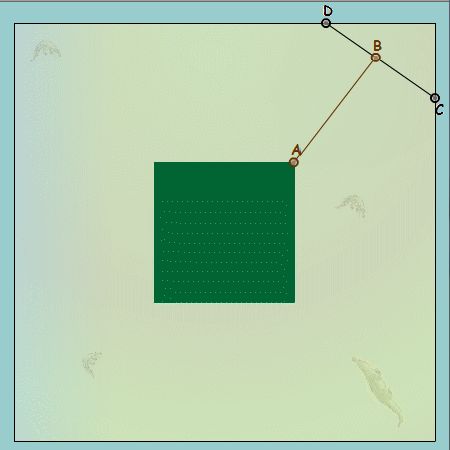
En fait deux barres vont suffire ;-) Pour faciliter la recherche j'ai attaché les 2 barres. B se déplace sur [CD].
Les segments sont de longueur constante respectant le rapport de 9,50 mètres de longueur pour 10 mètres de largeur de la bande d'eau.
Déplacer chacun des points A, B, C et D pour trouver une solution.
On peut déplacer les points avec la SOURIS ou bien avec le CLAVIER.

On sélectionne d'abord le point à déplacer avec la souris.
D, C et A peuvent être déplacés avec les qutre flèches Gauche, Droite, Haut et bas.
B peut être déplacé avec les flèches Gauche et Droite.

 

 

Un message s'affiche dès que l'on trouve une solution.
Attention, le résultat est très précis. Il y a très très peu de marge...
Commencer le déplacement des points avec la SOURIS et affiner avec le CLAVIER.

 

 

 

 

Solution

Proposer quatre barres, ne fait que troubler car deux barres suffisent.
Par ailleurs chacun sait que le chemin le plus court entre deux droites s'obtient avec une perpendiculaire commune à ces deux droites.
On a donc bien du mal à imaginer une solution qui utilise une ligne oblique...
Toutefois, lorsqu'on fait les calculs avec le théorème de Pythagore on réalise qu'il y a très peu d'amplitude pour placer les barres.
Bien entendu, les deux barres sont initialement placées sur le pourtour et non sur l'île ;-)

Quelle est la plus petite longueur possible pour chaque barre avec les mesures données ci-dessus :
île de 10m de côté et mare de 30m de côté ?

Ci-dessous l'une des 8 solutions.


                                                                                                                     

Réponse

La réponse est environ 9,428 m, exactement 20/3 m. Il y a donc très peu de jeu pour placer les barres.

De façon générale pour une île de côté c et une marre de côté 3c, nous obtenons une barre de longueur minimum 2c/3 m.

Explication

Une solution symétrique est optimale.
Le carré du coin ABCD est de côté c.
Sa diagonale mesure DB = c.
En partant du coin B, c'est la distance minimale que nous devons obtenir avec les barres pour ne pas tomber à l'eau.



Soit lg la longueur d'une barre.
Soit I le milieu de PR.

Dans le triangle rectangle isocèle PBR, nous obtenons
IB =PR/2   soit   IB = lg / 2

DI + IB = lg + lg/2 = 3*lg / 2.
Il faut donc
3*lg / 2 > c

et enfin       lg > 2c/3 .