Le cube diamanté

Le diamant intérieur transparent : CLIQUER

Le cube
Le diamant
Le diamant dans le cube
Le dodécaèdre rhombique
Le patron et la démonstration et le nid d'abeilles...

Le cube

Ci-dessous deux cubes l'un est transparent l'autre opaque.

CLIQUER chaque image ci-dessous pour l'animer le cube en dimension 3 :

Le cube est composé de 6 faces qui sont des carrés. Il a 8 sommets et 12 arêtes. Il a 3 arêtes en chacun des sommets.
Chez les grecs, il était le symbole de la Terre.

Nous allons transformer ce cube en une sorte de diamant spécial :
-fermé il aura l'air d'un cube classique mais il renfermera 6 pyramides dont les sommets coïncideront au centre du cube.
-ouvert ce sera un rhomboèdre, appelé aussi dodécaèdre rhombique, d'un volume égal au double de celui du cube.
Dans l'animation ci-dessous, quatre tiges sont fixées sur chaque face du cube, pour former les pyramides.
Cinq seulement des six faces sont représentées pour permettre la visualisation de l'intérieur du cube refermé.

CLIQUER

Les solides suivants ne sont pas necore pris en charge apr Ruffle... Patience.

Le diamant

C'est un cube dont chaque face supporte une pyramide composée de quatre triangles isocèles et d'une base carrée. Ce solide est un dodécaèdre rhombique. Nous l'animerons ci-après.

transparent opaque

Le diamant dans le cube

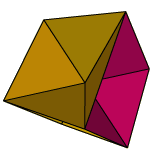
Ce solide complète le précédent. On l'obtient en retournant le solide précédent : les six pyramides sont enfermées dans le cube. Cela nous donne une approche du volume de chaque pyramide : 1/6 ème de celui du cube.


               transparent                                       opaque

Le dodécaèdre rhombique

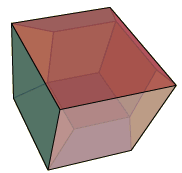
Choisissons deux faces carrées F1 et F2 ayant une arête commune [AB]. Les sommets S1 et S2 des pyramides placées sur F1 et F2 sont dans le même plan que A et B (ils sont le centre de deux cubes plaqués sur les faces F1 et F2). Joignons les points A, B, S1 et S2 ; nous obtenons un losange ABS1S2.
Nous trouvons de cette façon 12 losanges qui constituent un dodécaèdre rhombique. Vous trouverez l'un de ses patrons à la fin de cette page.



        transparent                                             opaque

Le patron et la démonstration

Les calculs
Soit c la mesure de l'arête du cube.
Calculons le côté du triangle isocèle SAB.
En utilisant le théorème de Pythagore dans les triangles rectangles SOI puis SIB,
nous avons SI² = SO²+OI² donc SI² = c²/4 + c²/4 soit SI² = c²/2
puis SB² = SI²+IB² donc SB² = c²/2 + c²/4 soit SB² = 3 c²/4

Finalement SB = c 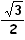c'est à dire environ 0,866 c.

LE NID D'ABEILLES
Pourquoi les cellules à miel dans une ruche ont-elles la forme de dodécaèdres rhombiques ?
Prenons c = 1
Avec le théorème de Pythagore dans le triangle SIB nous obtenons,
SI = .
L'aire du triangle ABS est .
L'aire du dodécaèdre rhombique est 24 soit 6 soit environ 8,48.
Le volume de ce dodécaèdre rhombique est 2 (deux fois celle du cube de base).

Pour un même volume,
l'aire d'un cube est environ 9,524.
Le rapport des deux aires est d'environ 0,89.
Pour un même volume, l'aire du dodécaèdre rhombique est plus petite que celle du cube.
Pas folle... l'abeille !
Ainsi les cellules à miel dans une ruche d'abeilles en forme de dodécaèdres rhombiques
nécessitent moins de cire pour leur fabrication que si elles avaient une forme cubique.

Pour construire le patron du cube diamanté d'arête c,
- choisir un patron parmi les 11 patrons du cube.
- construire 6 cercles de rayon R = c 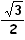soit environ 0,866 c.
- reporter dans chaque cercle le côté vert comme indiqué ci-dessous.
- découper en gardant les arcs verts autour des triangles isocèles : ils serviront de pattes de collage pour chaque pyramide.

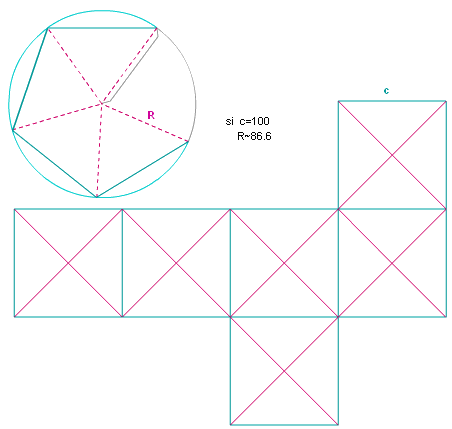
En repliant le patron de telle façon que les pyramides soient à l'extérieur nous obtenons le rhomboèdre, tandis qu'en le repliant pyramides vers l'intérieur, le cube se referme sur les six pyramides.

Voici maintenant un patron du rhomboèdre ou dodécaèdre rhombique obtenu avec les douze losanges.

Créez maintenant un jeu optique en décorant
de bandes de papier de couleurs différentes
ou de traits le cube vide.