Le problème

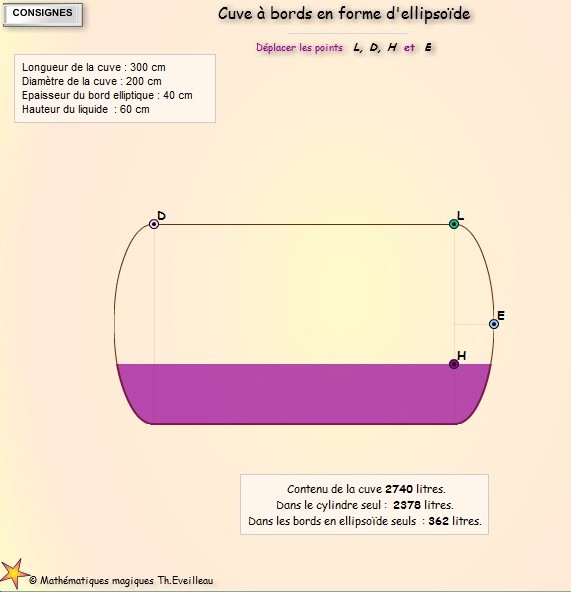
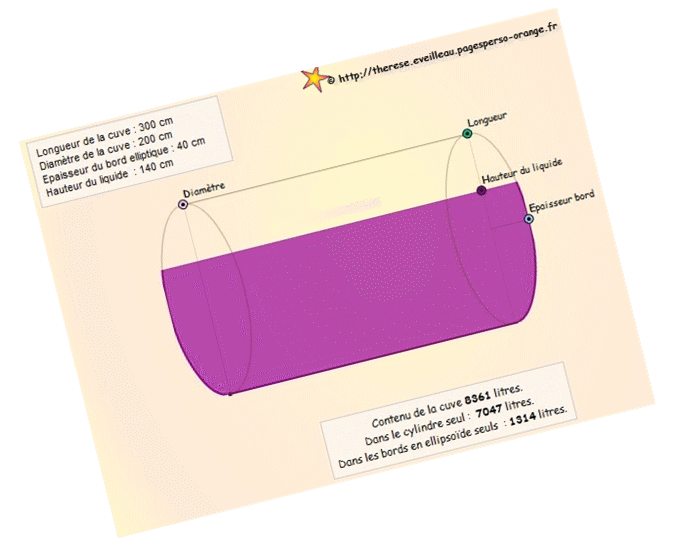
Cette fois la cuve possède des bords en forme d'ellipsoïde.
Attention, il est rare d'avoir un bord en ellipsoïde parfait. Cela peut impliquer de légères différences avec votre cuve.

Elle est donc un peu plus grande que celle en forme de cylindre et nous allons tenir compte des bords arrondis.
En déplaçant les points D, L, H et E, on peut déformer la cuve et visualiser les capacités correspondantes.
L --> la longueur de la cuve ;
D --> la hauteur de la cuve, c'est-à-dire le diamètre du disque de base du cylindre central ;
H --> la hauteur du liquide dans la cuve ;
E --> l'épaisseur du bord arrondi en forme d'ellipsoïde.

Les résultats sont obtenus à partir de la réduction de la cuve en grandeur réelle. Ils sont arrondis à l'unité près.

Cliquer

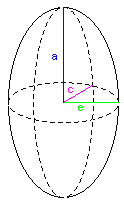
Le volume d'un ellipsoïde entier est donné par la formule

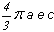Dans la programmation suivante, le calcul du contenu partiel de l'ellipsoïde est réalisé en utilisant le volume d'une calotte sphérique de hauteur h, de rayon R donné par la formule :
Vs (h) = π * ( h² / 3 ) * ( 3*R - h )

Il s'ensuit que le volume de la partie ellipsoïde de hauteur h et d'épaisseur e est : Vs (h) * e * R.


L'animation donne le tableau des résultats au litre près avec des dimensions variables entrées au cm près.

Dans cette deuxième animation, les dimensions peuvent être plus grandes.

ATTENTION chaque entrée numérique faite avec le clavier doit être validée avec la touche ENTREE.

Remarque : si l'épaisseur d'un bord est égale au rayon du cylindre, nous avons le cas particulier de bords en demi sphère : voir aussi ICI.

Dans cette animation, on peut imprimer un tableau des résultats obtenus cm par cm.
Pour enregistrer le tableau dans un fichier, il suffit de faire clic droit puis sélectionner tout,
puis copier et enfin coller dans son traitement de texte préféré.

 

Cliquer