Les carrés magiques de Dirichlet
et les températures...

Le problème : des figures magiques particulières à trouver.

Ce jeu est une modélisation simplifiée du problème de la propagation de la chaleur. Une maison est constituée de plusieurs pièces disposées dans un quadrilatère. Chaque pièce est bordée par plusieurs autres ayant une certaine température indiquée en rouge foncé. Nous connaissons la température à l'extérieur, près de chaque fenêtre. Cette température reste constante dans le problème. Initialement chaque pièce est à 0°. Nous savons que chaque pièce tendra vers une température stable.

Quelle sera la température finale de chaque pièce dans chacun des cas proposés ci-dessus ?

ANIMATION et résultats

La température de chaque pièce tend à se stabiliser
La valeur obtenue est logiquement comprise (au sens large, c'est-à-dire extrêmes compris) entre le maximum et le minimum des nombres qui entourent le carré.

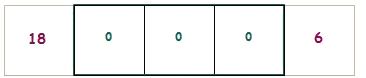
1°) Dans le premier cas les températures diminuent régulièrement de gauche à droite :
ce seront : 18, 15, 12, 9 et enfin 6.
Chaque case verte est la moyenne arithmétique de ses deux cases voisines :
15 = (18 + 12 )/2 ;
12 = (15 + 9 )/2 ;
9 = ( 12 + 6 )/2




2°) Dans le deuxième cas les températures nous aurons : 15 et 5 .
Chaque case verte est la moyenne de ses quatre cases voisines :
12 = (18 + 10 + 15 + 5 ) / 4 ;
5 = (12 + 1 + 1 + 6 ) / 4

Pour obtenir ces valeurs on peut poser x, pour la première valeur et y pour la deuxième.
Nous aurons
x = ( 18 +10 + 15 + y )/4
ET
y = (x + 1 + 6 + 1)/4.
Ce petit système de deux équations à deux inconnues nous mène simplement à la solution unique :
x = 12   ET     y = 5 .

Mais ce n'est pas toujours aussi facile...

3°)
Nous désirons que chaque case soit la moyenne des quatre cases qui l'entourent :
les quatre cases qui la touchent par un côté.

Ce n'est pas si simple à résoudre.

On peut résoudre un système à 9 équations et 9 inconnues...
Voir la résolution générale ici (pour les plus experts et les plus tenaces ;).

Retrouvez d'autres résolutions de ce système chez Diophante.fr à cette adresse :
http://www.diophante.fr/problemes-par-themes/arithmetique-et-algebre/a2-algebre-elementaire/4356-a2801-propagation-naturelle

On peut aussi approcher la solution petit à petit comme dans l'animation suivante.
La méthode choisie dans l'animation suivante consiste à approcher petit à petit la valeur optimale.
Pour cela, nous calculons (du moins l'ordinateur), la moyenne des quatre cases qui entourent celle qui nous intéresse.
On continue de proche en proche.
Quand tout est calculé on recommence de la même façon, case par case nous recalculons la moyenne de celles qui sont autour.

On s'arrête lorsque les valeurs restent stables.

Mathématiquement, nous savons que nous avons TOUJOURS une solution et même que celle-ci est unique.

Ceci repose sur l'étude de suites majorées et minorées convergentes (*).


Dans l'animation suivante il est possible de modifier,

- la taille de la grille avec le bouton adéquat (utiliser les flèches de ce bouton).
- toutes les valeurs qui entourent le carré ;
- toutes les valeurs intérieures au carré.

Ensuite, cliquer ou non le bouton Ultra Rapide :
- s'il est coché les résultats seront quasi instantanés ;
- s'il est coché, on peut observer l'évolution des résultats ;
  -> modifier éventuellement la vitesse avec le curseur en dessous des boutons.

Les résultats sont arrondis : en effet, la stabilisation des résultats peut être longue.
La machine, par exemple, peut afficher 5.99999... au lieu de 6 qui ne sera atteint qu'au bout d'un temps infini.

CLIQUER

 

(*)  Pour en savoir plus... visualiser complètement, ou en partie selon votre niveau,
l'excellente vidéo de Olivier Druet ICI.

Question indiscrète et logique :

Olivier Druet est-il réellement gaucher comme on voit sur la vidéo,
ou bien
a-t-il comme Léonard de Vinci de réels talents pour écrire "en miroir " ?

Réponse technnique ici dans cette vidéo sur le lightboard :
http://video.math.cnrs.fr/le-lightboard/

                       

---